33852 MATEMATYKA169

VI. Cią%i i szeregi funkcyjne

328

H    O    K

a₀ = -Jf*(x)d\=^ Jxdx+^Jod\ = -~,

-*    -n    O

a„ =^J^(x)cosnxdx=-iJxcosnxdx = —f-sinnx+4,cosnxj = -*    _n    L    n J-*

=-^-(l-cosnit)=-L(l-(-l)") dla 0=1,2,....

7tn    nn

Analogicznie obliczamy współczynniki b_n i otrzymujemy:

b„=Hr'^

Stąd dla każdego xe<-7t,7t> mamy:

w i

icn

f(x) =    +£Hj(!-(- |)")cosnx +(-!)"' Isin nx).

n=»l

Ponieważ f*(x) = f(x) dla x €(-*,*). więc dla x €(-*,*) mamy:

<0 -

^f(x)=~+2(-L(l-(-¹)")cosnx+(-l)"^+lisinnx)

n=l ¹⁰¹    0

Wiemy już, że otrzymany szereg jest zbieżny dla każdego xeR. Suma S(x) tego szeregu na zbiorze R jest funkcją okresową o okresie 2rc, przy

czym S(x)= f*(x) dla x €<-*,*>. Mówimy, że funkcja S(x) jest

okresowym przedłużeniem funkcji f* na zbiorze R Rysunek 4.5 przedstawia wykres sumy S(x) tego szeregu na przedziale <-3*,5tc>.

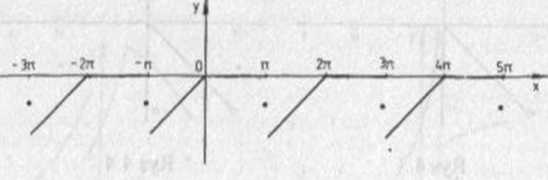
Rvs 4.5

Rozwinięcie w szereg Fouriera według sinusów LUB WEDŁUG COSINUSÓW.

1)    Załóżmy, źc funkcja f spełnia warunki Dirichlcla na przedziale <-t,t> i jest funkcją nieparzystą Wówczas wszystkie współczynniki a_n są równe zeru (uwaga 1). a zatem

f(x) £b_nsin-*- dla x«-U>

n»i

Mówimy wówczas, że funkcja f ma rozwinięcie w szereg Fouriera według sinusów.

2)    Załóżmy, że funkcja f spełnia warunki Dirichlcta na przedziale <-t,t> i jest funkcją parzystą Wówczas wszystkie współczynniki b_n są równe zeru (uwaga 2), a zatem

f (x)=a„ cos^f dla x 6<—t,t >.

~ n I

Mówimy wówczas, że funkcja f ma rozwinięcie w szereg Fouriera według cosinusów

PRZYKŁAD 4.2 Funkcję f(x) = 3 dla xe(0,w), (rys 4.6). rozwiniemy w szereg Fouriera według: a) sinusów, b) cosinusów.

Budujemy funkcję pomocniczą f* nieparzystą, spełniającą warunki Dirichlcta na przedziale <-n,n> i równą funkcji f na przedziale (O.rc), (rys 4 7) Zatem

dla

dla

dla

-3

3

0

f(x) =

x <=(-*,0), xe=(0.n),