40680 skanuj0109 (22)

B. Cieślar

Rys. 5.2.2

Podstawiając h = 2b otrzymujemy: b> 15 cm.

Przyjmując b = 15 cm i h = 30cm maksymalne naprężenia będą równe: _maxa- 10 MPa.

Belka o trójkątnym przekroju poprzecznym (rys. 5.3.1) została obciążona

dwiema siłami. Określić niezbędne wymiary przekroju, jeżeli: P = 120 kN, fdcg 20 MPa, f* = 5 MPa, I = 8 m.

ET

&

V. Zginanie ukośne

CL~~CC

I / 2

1/2

1/3

Rys. 5.3.1

Rozwiązanie

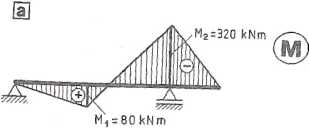
Wykres momentów zginających pokazano na rys. 5.3.2a. Momenty bezwładności przekroju wynoszą:

J = —,    J_v=—.

^x 72 ^y 24

Największe naprężenia wystąpią w przekroju, w którym działa moment zginający M=+80 kNm lub w przekroju, w którym działa moment M = -320 kNm.

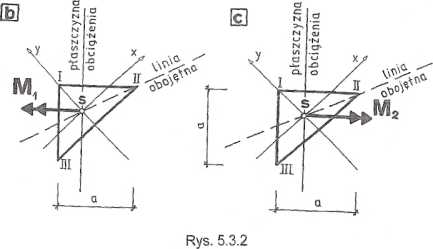
Przekrój obciążony momentem M = 80 kNm (rys. 5.3.2b), a = 135°: M_x = M cos135° = M^; M_y = M sini 35° M