42499 P1080266

czona przez poszukiwanie wśród sąsiadów wybranej komórki (nazywanej bieżącą) I takiej, która ma wagę o jeden mniejszą, Następnie ta komórka staje się bieżącą I i proces poszukiwania drogi odbywa się iteracyjnie, aż zostanie znaleziona droga I do celu. Optymalna droga to droga najkrótsza przebiegająca przez wszystkie ko- I mórki bieżące.

Zastosowanie metody propagacji fal jest ograniczone do środowisk stacjo- I namych i zamkniętych. Podczas implementacji metody ważny jest sposób dys- I kretyzacji przestrzeni konfiguracyjnej. Liczba komórek elementarnych powinna I być umiarkowana.

6.5.2.    Metoda diagramu Woronoja

Metoda diagramu Woronoja jest metodą planowania bezpiecznych torów robo- I tów mobilnych poruszających się na płaszczyźnie. Zwykle bywa wykorzystywa- I na w środowisku o niezbyt licznych przeszkodach stacjonarnych. Planowanie I przebiega w dwóch fazach. W pierwszej, na podstawie mapy otoczenia robota, ■ w której znajdują się przeszkody, nanosi się krzywe równoległe do przeszkód. I Dla przeszkód w kształcie wielokątów krzywymi są odcinki lub łuki parabol. I Łukom powstałego grafu są przypisywane wagi równe długościom torów między I wierzchołkami mierzonym wzdłuż linii równoodległych od przeszkód (odległość I ta jest zazwyczaj dłuższa od odległości euklidesowej między wierzchołkami).

W drugiej fezie planowania jest przeszukiwany utworzony nieskierowany graf, I np. wg algorytmu Dijkstry, w celu znalezienia najkrótszej drogi łączącej wierz- I chołek początkowy z końcowym.

Główną zaletą metody diagramu Woronoja jest bezpieczeństwo wyniko- I wego toru ruchu, tym bardziej że informacja o odległościach od przeszkód (ko- I nieczna podczas tworzenia linii równoległych od przeszkód) może podwyższać I wagi niektórych łuków. Jednakże może prowadzić do torów nawet przesadnie I bezpiecznych, a przez to zbyt długich. Do wad metody należy zaliczyć trudność I w uwzględnieniu zmian środowiska, np. w wyniku ruchu przeszkód. Czasem I także najkrótsza droga w grafie niekoniecznie musi być łatwa do realizacji przez I poruszającego się robota. Z tego powodu warto wybrać kilka torów porówny- I walnych z optymalnym pod względem długości i dopiero z nich wybrać do re- I alizacji najlepszy, jeżeli chodzi o kryterium jakości rozszerzone o liczbę i trud- 1 ność zakrętów toru.

6.5.3.    Graf widoczności

Metoda bazująca na grafie widoczności ma, w pewnym sensie, własności kom- I plcmentame do własności metody diagramu Woronoja. W metodzie tej planuje I się efektywnie optymalny tor ruchu robota mobilnego na płaszczyźnie, na której 1 znajdują się jedynie przeszkody o kształcie wieloboków wypukłych. Tworzony I 178 graf konfiguracji powstaje przez łączenie wierzchołków, których incydencja jest '

określona na podstawie kryterium widoczności. Wierzchołkowi początkowemu jest nadawana ocena równa zeru. Wierzchołek docelowy jest traktowany jako wierzchołek przeszkody. Rozpoczyna się od wierzchołka początkowego. Bieżący wierzchołek, wybrany na podstawie oceny jego jakości, jest łączony gałęziami z wierzchołkami przeszkód widocznymi z rozwijalnego wierzchołka. Relacja widoczności oznacza bezkolizyjność toru miedzy parą wierzchołków, a gałęzi je łączącej jest przypisywana waga równa długości euklidesowej toru miedzy nimi. Metoda grafu widoczności jest na tyle efektywna czasowo, że może być stosowana nawet w trybie czasu rzeczywistego z ruchomymi przeszkodami, o ile tylko mapa otoczenia robota jest uaktualniana odpowiednio często. Bardzo dobre efekty uzyskuje się w połączeniu z metodą elastycznej wstęgi.

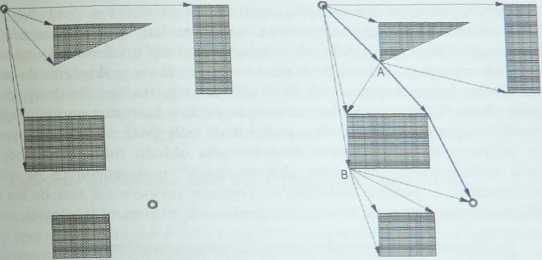
Rysunek 6.^_____

Rozwinięcie wierzchołka początkowego i rozwinięcie wierzchołków oznaczonych literami A i B oraz tor wynikowy

Kryterium efektywności ruchu jest długość euklidesowo toru, a algorytm implementujący metodę przebiega wg następującej procedury - rys. 6.10:

Krok 1. Wczytać wierzchołek początkowy i końcowy ruchu i układ przeszkód. Wierzchołek początkowy przyjmuje wartość równą zeru, natomiast wierzchołek docelowy jest traktowany jak wierzchołek przeszkody.

Krok 2. Rekurencyjnie, rozpoczynając od wierzchołka początkowego, budować graf widoczności. Bieżący wierzchołek, wybrany na podstawie oceny jego jakości, jest łączony gałęziami z wierzchołkami przeszkód widocznymi z rozwijanego wierzchołka. Relacja widoczności oznacza bezkolizyjność toru między parą wierzchołków, a wierzchołkom gałęzi je łączącej jest przypisywana waga równa długości euklidesowej toru między nimi. Gdy wierzchołek cu, będący końcem gałęzi, jest wygenerowany po raz pierwszy, uzyskuje ocenę równą sumie gałęzi do niego prowadzonej i oceny wierzchołka będącego początkiem tej gałęzi. Jeże-

179