42796 Strona6

= 0.

Stąd:

(14) ..    / A² +B² +C* = a.

Stosując wzór (1.7) i uwzględniając (12) i (14), otrzymujemy:

J =. j j (y -f 2 -{- y a² — *^J) dS = j j (a sin 9 -f z + V a² — (a cos ę)²) a dędz = s    j'

= a\\(a $w 9 + z + aVsin²p) dędz.

I    ^J

Wyliczamy kolejno całki;

k 2k

/_x = a j J o sin 9 dz dę = a² $ [ J sin 9 dę] dz = 0,

A    0    0

A ■■

J₂ — ajj z dtp dz a a\[J zdę\dz itah², j    00

/, = a² J 5)/"sin² $> <fe = a² J $ | sin 91 dę dz =

- . * ^J 2n    h    2*    •    K    2*

= a² S(|sin 9\\dz]dę <= J | sin ę>| dtp = a²/i(S|$in ęjdę -f- j | sin ę| dę)=

0    o    O    Ok

r.    2*

= a²h ($ sin 9 dtp -f- j (— sin 9) dę) = Aa'h.

o    K

stąd:

	cx	Iz.
c a	dę	o?
V ^a	dx	8y
	dz	dz

— osin 9 o cos 9 0 0

/ = J_x -f J₂ 4. -/j uch* H- 4a^JA = oA(4<2 -|- rJt).

Zadanie 1.6. Znaleźć współrzędne środka ciężkości x_e, y_r, z_e górnej powierzchni kulistej X¹ -f y² + z² = R², z> 0, której gęstość powierzchniowa w każdym punkcie równa się odległości tego punktu od osi Oz.

Rozwiązanie. Określamy powierzchnię S równaniami parametrycznymi: x = R cos ę cos O,

(1)    y = R sin 9 cos 9, R>0,

z = R sin €>,

gdzie:

(2)

Z treści zadania wynika, żc-.cęstość powierzchniowa p(x, y, z) określona jest W70rcm:

K^x,y.=) — 1'a* +>•'.

Masa m, zgodnie z wzorem (I.1J), określona jest całki]:

(3)    ni — ? J\'x⁷ -i- y^: dS.

’s

W zadaniu 1.4 wyliczono, że dla powierzchni S określonej równaniami (I):

(4)    dS = R² cos 0 dę d0.

Wyliczamy teraz całkę powierzchniową (3) zgodnie z wzorem (1.7), uwzględniając pr*y tym (1) i (4). Mamy;

*:

2

m » jj R cos O R¹ cos O dt? dO = R³ j dę f cos² 0 dO ^

j    aa.

(5)

2*/t³

1* 1 — cos 20    n^zR³

) - — — </o--₂-

o

7e względu na symetrię    A/_i: — 0. Zatem x_c = y_e = 0. Obliczamy moment

statyczny M_ft, według wzoru (1.12):

(6)

Afj, — J i z J^jr¹ t y- dS — J j R sin 0 R cos O R² cos O dę dO -s    *

. £

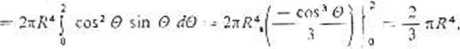
Wstawiając (5) i (6) do wzoru (1.13) otrzymujemy, te:

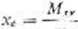
ni

4_

3-

R.

Zadanie 1.7. Obliczyć moment bezwładności jednorodnej powierzchni stożkowej * —-bjż.tlla ^v? -• y³**X', względem początku układu współrzędnych.

Rozwiązanie. Oznaczamy prz.ez p (p stale) gęstość powierzchniowa. Zgodnie z wzorem (1.16) szukany moment określony jest całką powierzchniową postaci:

(1)    A --    -f y^ł z^:)d.\\

Łatwo wyliczamy, żc:

(2)    dS =■ |M ! ^ ! ^7 dx dy    J / 1 Jj\ dx Jy.

Wstawiając (2) do (I) i uwzględniając, że z = - I .v^ł — r\ manty: 7 — Cwlcacr.Sa ? analizy

07