62963 skanuj0016 (36)

172 4. DYNAMIKA MASZYN I MECHANIZMÓW Z CZŁONAMI SZTYWNYMI

172 4. DYNAMIKA MASZYN I MECHANIZMÓW Z CZŁONAMI SZTYWNYMI

•1 Oi

czyznach korekcji I i II na promieniach = 50 mm i r#2 = 40 mm. Pozostałe dane są następujące: m-j = 2 kg, r-j =10 mm, 7W2 = 3 kg,

= 15 mm, ff?3 = 2 kg, 2*3 = 12 mm, = 4 kg, 2*4 = 20 mm. Odległości między masami wynoszą: l12 ⁼ ^23 ⁼ ^34 ⁼ 100 mm* Zakładamy, że wszyi kie masy leżą w jednej płaszczyźnie oraz wyważenia należy dokonać z* pomocą dwóch mas:    -| i w^2*

Rozwiązanie. Ponieważ siły bezwładności mas i przeciww: powinny znajdować się w równowadze, wartości mi możemy określić z warunków (4.114).

Układając równania momentów statycznych względem punktów 0₁ i 0₂, otrzymujemy względem punktu 0-j wyrażenie

*3 ^r3 ^Z34 ⁺

u

34

1 ^X1

<*12 ⁺

23

'34'

^Jd1 ^rd1 <*12 ⁺ *23 ⁺ *34* ’ °*

Podstawiając wartości liczbowe, otrzymujemy

2*12*100 + 3*15*200 - 2*10*300 _ _n ^ ^md1 1 - 50-3Ó0-~ '’S°'^{36 kg}‘

Z równania momentów sił względem punktu 02 będzie

4*20*300 - 2*12*200 - 3*15*100 _ .    .

^md2    40*300    ^1,225 kg.

Jeżeli po obliczeniach otrzymujemy znak minus, oznacza to, że przeciwwagę należy ulokować po przeciwnej stronie niż założono.

PRZYKŁAD 4.23. Dany jest układ wirujący o rozkładzie mas jak na rys. 4.41. Należy układ ten wyważyć dynamicznie przez dodanie dwóch mas: mj i mjj, ulokowanych w płaszczyznach korekcyjnych I i II na promieniach pj = p_IX = 100 mm pod kątami aj i a_XI. Dane: masy m-j =

= 10 g, = 15 g, m3 = 20 g, m4 = 10 g, promienie r-j = 50 mm, 2*2 = = 40 mm, 2*3 = 60 mm, r4 = 50 mm. Odległości pomiędzy masami l-\2⁼

= l23 = 734 = l. Kąty aj i ajj należy odmierzać od linii 0x w lewo.

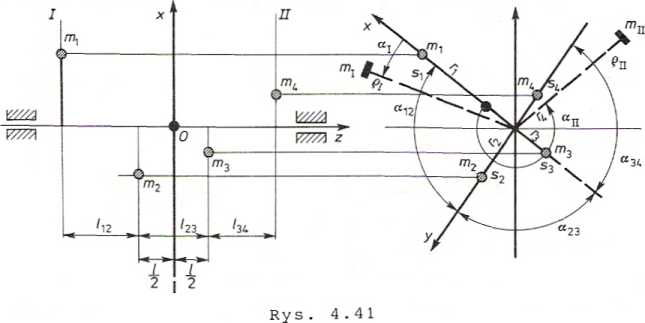
Rozwiązanie. Przyjmujemy układ współrzędnych Oxyz jak na rysunku co w tym przykładzie upraszcza równania, gdyż zerują się