69535 skanuj0010

jnrunku rezonansu wynika, że

1

coC

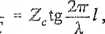
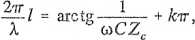
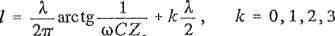
Impedancję falowa dla linii kablowej (rys. 14.8b) wyznacza się ze wzoru

ln— = 62,4X1,

Z =    = 62,4X1,

fir ^ri

l = (7,4+£-15) m.

jimalna długość linii dla k = 0, przy której występuje rezonans, wynosi l = 7,4 m.

Zadanie 14.8

Do zacisków źródła napięcia sinusoidalnego o impedancji wewnętrznej Z, została uczona koncentryczna linia kablowa bezstratna, rozwarta (rys. 14.9a). Należy obliczyć imalną długość linii, przy której w obwodzie występuje rezonans. Przekrój koncen-Iznęj linii kablowej przedstawiono na rys. 14.9b. Dane: /=5MHz, R = 10X1, i- 10 pF, r, = 2 mm, r₂ = 16 mm, e_r = 4.

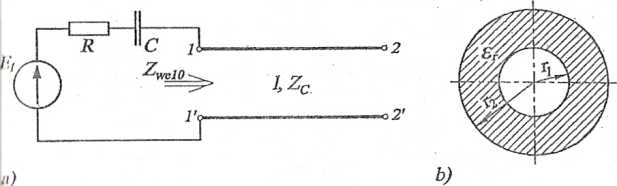
Rys. 14.9

Odpowiedź

X = — = 30 m,

ffir

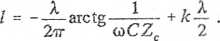
Dla k = 1    = 9,75 m.

«f^r"

Przykład 14.9 i

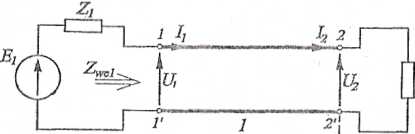
Bezstratną, napowietrzną linię długą, podaną na rys. 14.10, obciążono impedancją Z₂. Należy obliczyć napięcie i prąd na początku i na końcu linii. Dane: E_l=jl00V, Z_x = (100+; 100)0, Z₂ = (100-/100)0, / = 10 m, /= 30 MHz.

x i -1

Rys. 14.10

Rozwiązanie

Równania określające rozkład napięcia i prądu wzdłuż linii bezstratnej dla odległości r liczonej od końca linii mają postać

UQc) - U₂cos(3x + jZ_cI₂smfix,

XJ₂

I(pc) = j smfix +1₂ cosf)x,

Zc

gdzie p =    .

/

Dla rozważanego przykładu \    ^ = 10 m = /, stąd dla x = / = A. impedancja wejściowa

U_t

7    = _1 _ 7

^we 1    -^2 •

Prąd /j można wyznaczyć z zależności

= j 0,5 A,

Z, +Z

1 we

a następnie napięcie

U_x = Z_mlI_x * (50+/50) V.

Napięcie i prąd na końcu linii po przekształceniu równań linii dla x = /

A

cos pi    -jZ_eswpi

-j    sin pł    cos pi

*1

A

cos2ir -/Zcsin2ir		*|	1
		50+/50	(50+/50) V
sin2ir coś2ir		. J ~	j0J5A