73561 Image50 (13)

98

Z treści zadania wynika, że punkt porusza się po powierzchni

= 1,

2 2 2 x y    z^z

-    ——    -L-    —

a² ^ b²    c²

gdzie: a, b, c - stałe.

Stąd równania Lagrange’a pierwszego rodzaju mają postać:

m x

= 2X

a

2 »

b²'

m y = 2X

m z

= 2X

Mnożąc pierwsze z tych równań przez x, drugie przez y, trzecie przez z i dodając stronami otrzymujemy

• •• • •• • •« -(xx + yy + zz) = /l

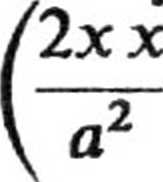
2yy    2 zz

b² + c²

m

Różniczkując równanie elipsoidy otrzymujemy

2xx

+

a

2 yy

b²

+

2zz

0.

Stąd

0.

xx 4- yy 4- zz

Korzystając z własności pochodnych wynik ten możemy zapisać w postaci

1    d

2    Jt

(x² + y² + z²) = 0

,*.2

:2

*

Wyrażenie w nawiasie jest kwadratem prędkości punktu. Wobec tego

i

d

dt

v² = 0,

c.

r

1

i ostatecznie

v^z = const

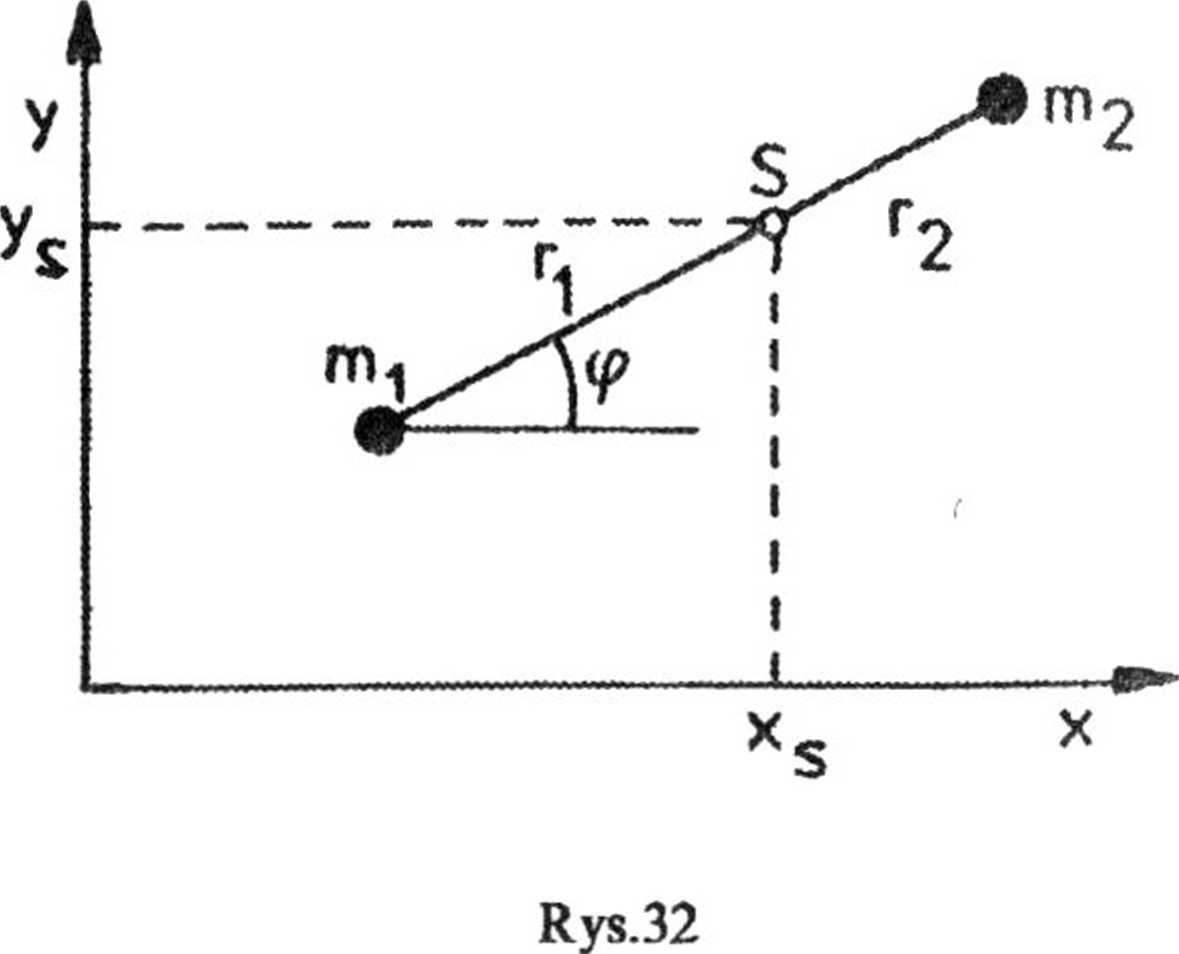
2.39. Z treści zadania wynika, że zaniedbujemy opory ruchu, wobec tego moment pędu układu jest stały, stąd ruch jest płaski. Przyjmujemy układ współrzędnych, tak aby płaszczyzna (x, y) była płaszczyzną ruchu

(rys.32).

Wówczas układ ma trzy stopnie swobody. Odpowiadającymi im współrzędnymi uogólnionymi są współrzędne x₅ i y_s środka obrotu i kąt (p nachylenia pręta do osi x.

Energia kinetyczna układu

\ m, (x² + y\) +

+ 2 ^m2 + yl),

gdzie: x_i, y_t - współrzędne masy m_t, x₂, y₂ ~ współrzędne masy m₂. Ale

x_x = x, - r_i cosę?,

y i = y_t

r_i sin(p,

^x2 — ^Xs + ^r2 ^cos</⁾»

y₂ = y_s + ^r2 ^sin<p-

Wobec tego

E_t =

+ m₂ 2

(X,² + yj) +

^ml^rl + ^m2^r2 *

<P

Energia potencjalna

0.

E

2