121014

rO) = -

T, S‘(s)

m-i,

Obliczmy poszczególne składniki powyższego wzoru

Z treści zadania wynika, że siła tnąca T_y jest stała i wynosi P

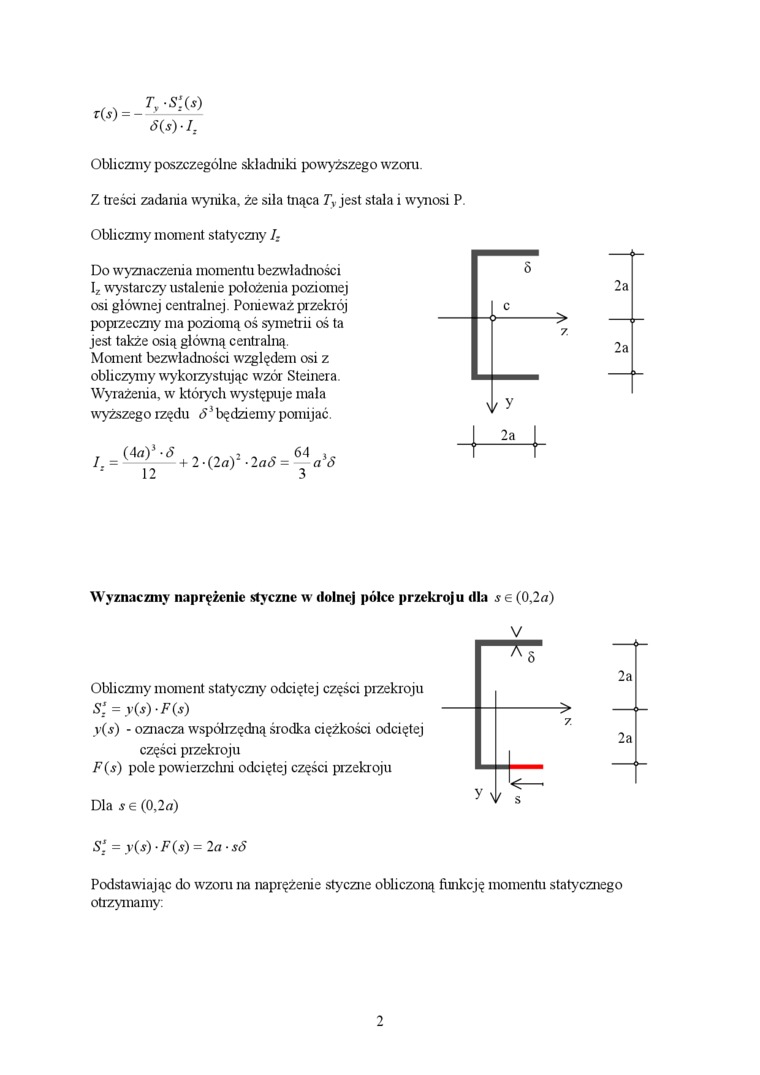
Obliczmy moment statyczny 1_:

Do wyznaczenia momentu bezwładności I₂ wystarczy ustalenie położenia poziomej osi głównej centralnej Ponieważ przekrój poprzeczny ma poziomą oś symetrii oś ta jest także osią główną centralną.

Moment bezwładności względem osi z obliczymy wykorzystując wzór Steinera Wyrażenia, w których występuje mała wyższego rzędu 5'będziemy pomijać

(4n)^J<5

12

+ 2 (2a)^! - 2aS =

	1 ^2a 1	!
	f 1	i

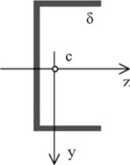
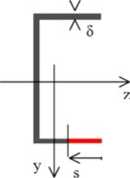
Wyznaczmy naprężenie styczne w dolnej półce przekroju dla ^ e (0,2/7)

Obliczmy moment statyczny odciętej części przekroju S‘ = y(s)F(s)

>■(s) ■ oznacza współrzędną środka ciężkości odciętej części przekroju

F(s) pole powierzchni odciętej części przekroju Dla se (0,2 a)

2a

2a

S' = y(s) ■ F(s) = 2n ■ sS

Podstawiając do wzoru na naprężenie styczne obliczoną funkcję momentu statycznego otrzymamy:

2