00098490

270

in. FUNKCJE ZMIENNEJ ZESPOLONEJ

Ze wzoru (111.73) wynika, że szereg potęgowy można wewnątrz koła zbieżności różniczkować wyraz po wyrazie.

Tw. (o zbieżności niemal jednostajnej). Szereg potęgowy Jest jednostajnie zbieżny w każdym zbiorze domkniętym i ograniczonym, zawartym wewnątrz ko.a zbieżności.

W szczególności, jeżeli szereg (111,72) ma skończony promień zbieżności i?, to szereg ten jest jednostajnie zbieżny w domkniętym kole o środku z₀ i promieniu OR, gdzie fi jest dowolną liczbą z przedziału otwartego (0,1). W związku z tym' mówimy, że szereg (III.72) jest w swym kole zbieżności niemal jednostajnie zbieżny. Jeżeli R = +oo, to szereg potęgowy (III.72) jest jednostajnie zbieżny w domkniętym kok o środku r₀ i dowolnym promieniu r.

Funkcje całkowite. Jeżeli szereg potęgowy (IIJ.72) ma promień zbieżności R = +co, a więc jeżeli jest to szereg zbieżmy dla każdej wartości z, to jego suma jest funkcją określoną na całej płaszczyźnie otwartej. Funkcje takie mają ważne, znaczenie.

Def. Funkcja całkowita jest to suma szeregu potęgowego zbieżnego na całej płaszczyźnie otwartej.

Z twierdzenia o holomorficzności sumy szeregu potęgowego wynika, że funkcja całkowita jest holomorficzna na całej płaszczyźnie liczbowej. W dalszym toku wykładu zobaczymy, źe i na odwrót: każda funkcja holomorficzna na całej płaszczyźnie liczbowej jest funkcją całkowitą.

Rozważmy funkcję całkowitą

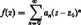
Jeżeli istnieje taka liczba n₀, że dla każdego n > n₀ mamy a„ «= 0, to funkcja całkowita jest wielomianem. Jeżeli liczba n₀ o wymienionej właściwości nie istnieje, a więc jeżeli szereg potęgowy, którego sumą jest funkcja/i(z), ma nieskończenie wiele wyrazów różnych od zera (dla z ^ z„), to j{z) nazywamy funkcją przestępną.

Pewne funkcje całkowite, a więc sumy szeregów zbieżnych na całej płaszczyźnie mają takie właściwości, dzięki którym wygodnie się nimi posługiwać w wielo zagadnieniach. Dla funkcji tych wprowadzamy specjalne symbole i nazwy, często takie same, jakich używamy w analizie funkii zmiennej rzeczywistej. Takie rozszerzenie znaczenia symbolu i nazwy musi być jednak tego rodząju, żeby w przypadku, gdy zmienna zespolona przyjmuje wartość rzeczywistą, było ono zgodne ze znaczeniem ustalonym dla rzeczywistych wartości argumentu.

SZEREGI FUNKCJI ZESPOLONYCH

271

Podamy teraz tego rodzaju rozszerzenie znaczenia nazw: funkcja wykładnicza przy podstawie e, funkcja sinus i funkcja kosinus. Określamy mianowicie

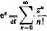
(III.74)

^SlnZ dfS¹- ^1)B (2n+1)!

(Ul-75)

ail.76)

Zauważmy, że dia rzeczywistych wartości * zmiennej z definicje te są identyczne ze znanymi rozwinięciami w szereg Macfaurina funkcji e*, sin* i cos*. Rozszerzenie znaczenia nazw i symboli tych trzech funkcji, dokonane za pomocą definicji (IIJ.74)-(111.76), jest więc prawidłowe. Nawiązując do rozwinięć w szereg Mac-laurina łatwo też udowodnić, że promienie zbieżności szeregów stanowiących prawe strony równości (111.74)—(111-76) są nieskończone. W tym celu wystarczy zauważyć, te kola zbieżności tych szeregów zawierają katdy punkt osi rzeczywistej, gdyż rozwinięcia* funkcji e*, sin* i cos* w szereg Maclaurina są zbieżne na całej osi liczbowej.

Z uwagi na określenie (HI.74), mamy dia urojonej wartości z —jy następujący związek

ML

Xr+iV r-ii

y**¹

(2n+l)J

e’’’ = cos y+j siny

czyli

(UŁ77)

a więc otrzymaliśmy znany skądinąd wzór Eulera.

Ponadto na podstawie schematu Cauchy'ego mnożenia szeregów mamy

o»-^ł \

(n—k)\ I

a więc jeżeli z <* x+jy, to

e* =    <nt 78)

Uwaga I. Jeżeli rówraSć (UI.77) oraz równość (ffl.78), w których *iysąto liczby

rzeczywiste, u-x+Jy, potraktować lącańt za definicję e*. to posługując się rozwinięciami funkcji siny. coty i e* w szeregi Maclaurina oraz korzystając ze schematu Caudiy’ego mnożenia szeregów,