00098489

268 in. FUNKCJE ZMIENNEJ ZESPOLONEJ

P>r|i>lrf I. Zbadać zbieżność Kr i-egu

Obliczamy granicy 2 według w.

i -

więc zgodnie za wzorem IHL69) mamy X - 1. Szereg (UI.70) jest więc zbielny (i lo bezwzględnie) dla |zl < 1, natomiast jest rozbieżny dla Iżl > I. Pozostało zbadanie zbieżności szeregu (01.70) na okręgu |z| — I kota zbieżności. Wykażemy, je w tym przypadku szereg (111.70) jest także zbieżny 1 lo bezwzględnie. W tym cdu bierzemy pod uwagę szereg utworzony z modułów wyrazów ner (HI.70) i podstawiamy I zamiast lfl. Otrzymamy

f ^

f=i*"

a więc szereg liczbowy o którym wiemy, że jest zbieżny. Wynika stęd, że azereg (111.70) jest zbieżny bezwzględnie dla |x| < ł, natomiast jot rozbieżny dla 'r| > I. Zauważmy jeszcze, że ponieważ dla każdego ac IV i dla każdego z ipeImającego warunek |zi < 1 jest spełniona nierówność

wicc'na mocy kryterium Wcierstrassa szereg (IU.70) jesl jednostą/nie Mrimy w kole zbieżności

1*1 < I.

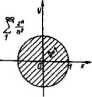
Koło zbieżności szeregu (01.70) jest przedstawione na ryi. Ol.il. Brzeg koła, zaznaczony ię ciągłą, należy tu do zbioru punktów, w którym szereg jest zbieżny.

Przykład 2. Zbadać zbieżność szeregu

|U (01.71) równa się I. Szereg jest więc bezwrzględ-ie zbieżny dla W < 1. natomiast rozbieżny dla lf) > 1. Na okręgu |*I - 1 koła zbietnołd szereg

011-71) nie zachowuje się jednakowo. Na przykład dla > - 1 szereg ten jol rozbieżny, natomiast dla z “ — 1 jest zbieżny. Pominiemy szczegółowe badanie szeregu (IH-71) na okręgu koła zbreżnoScr poprzestając na informacji, ie punkt z — I je»t jedynym punktem okręgu 1*1 = I • ^w którym szereg (III.7I) jest rozbieżny (rys. III. 12).

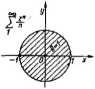
Rys. III. 12

Czytelnik bez trudu sprawdzi, że szereg

P

ma promień zbieżności miast szereg

+ oo, a zatem jest zbieżny na całej płaszczyźnie, nato-

ma promień zbieżności R =* 0, więc jest zbieżny tylko w punkcie z => 0.

Uwaga. Można udowodnić, że jeżeli istnieje granica (właściwa albo niewłaściwa) lim y fa.| ■» X

lo promień zbieżności X szeregu potęgowego (III.65) wyraża się a pomocą równości (111.69). Fakt ten notujemy zazwyczaj krótko w postaci A “ y; jest to tzw. wzór Cauchyego-Hadamarda. Należy przy tym pamiętać, łe Jł**0. gdy A - +oo, oraz K «■ + «, gdy A =■ 0.

Podamy teraz bez dowodu dwa twierdzenia o szeregu potęgowym, którego promień zbieżności jest różny od zera.

Tw. (o holomorCiczności sumy szeregu potęgowego). Suma S(z) szeregu po. ligowego

s

a.(z-zo)*

(III.72)

jest funkcją holomorficzną wewnątrz kola zbieżności (na całej płaszczyźnie, gdy R — +oo), przy czym

a ponadto szereg pochodny ma laki sam promień zbieżności jak szereg dany.

011.73)