70877 str034 (5)

34 I. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

Zadania do rozwiązania

1. Znaleźć promień zbieżności szeregu:

11=1    n= 1

d)

Ed + O"

(« + l)(n+2)

n— 1

(z-2)",

oo

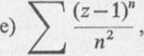
n— I

oo

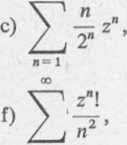
n= 1

g)

E3"(z-l)ⁿ V(3n—2)2"

2. Następujące liczby dane w postaci kartezjańskiej przedstawićwpostaci wykładniczej: a) z = 1,    b) z = -1,    c) z = i,

d) z = -/,    e) z = — 1 + /,    f) z = -~j=- -j=i,

g) z = V^{3 + ,}’> h) z = -2+2/.

3.    Znaleźć część rzeczywistą i urojoną liczby:

a) cos(l + i). b) tg(2—/),    c)sin(l+2/).

4.    Obliczyć:

a) ln(—/), Ln(—/), b) ln(-l-/), Ln(-1-/), c) ln(l — /), Ln(l — /).

5.    Znaleźć część rzeczywistą i urojoną liczb:

a) z =    b) z = <?*',    c) z = 2e~^Ki,

d) z = sin/, e) z = 3e**¹,    f) z = cos(2+/).

6. Wykazać, że moduły liczb: a) cos 2/, b) z = cos 3/ są większe od jedności.

Odpowiedzi

g) r = ^2/3.

1.    a) r = 1, b) r = e, c) r = 2, d) r = 1/^/2, e) r = 1, f) r = 1,

2.    Wskazówka: por. zad. 4.2:

a) z = e‘°, b) z = e^ln, c) z = e‘ⁱⁿ, d) z = e**, e) z = jle⁴*,

g). z = 2e'K h) z =

3.    Wskazówka: por. zad. 4.3:

a) Re(cos(l + i)) = ife+-^-jcosl, Im(cos(l + i))= ~i(e—i-Jsin 1,

b) Re (tg (2-/)) =

sin 4

c) Re (sin (1+2i‘)) =

2(cos²l + sinh²l) e² + e

, Im (tg (2-0) =

sinh2

2(cos²l+sinh²l)’

2

6 — 6

sin 1, Im (sin (1 + 2/)) = —r-cos 1.

2