str016 (5)

16 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

Zadanie 2.5. Do zacisków źródła prądu zmiennego o napięciu U dołączony jest odbiornik złożony z opornika o stałym oporze R i kondensator obrotowy o pojemności C zależnej od kąta obrotu a (rys. 1.2). Opornik i kondensator połączone są szeregowo. Wyznaczyć zespoloną wartość natężenia / prądu elektrycznego w odbiorniku w zależności od kąta a obrotu kondensatora, jeżeli jego pojemność C określona jest następującym wzorem:

C(a) = C₀a dla 0<a<7t, gdzie C₀ jest liczbą rzeczywistą dodatnią.

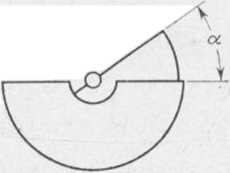
R

o-IZ=}-

°—rf-

m

Rys. 1.2

Rozwiązanie. Impedancja z odbiornika określona jest wzorem

a>C’

gdzie to>0 jest pulsacją prądu.

W rozważanym przypadku mamy

a)C₀oc

z = R —

Na podstawie prawa Ohma możemy napisać wzór określający natężenie I prądu elektrycznego jako funkcję zespoloną zmiennej rzeczywistej a

j UwC₀a o)RC₀a — i

Zadanie 2.6. W przewodniku o przekroju prostokątnym    oraz 0płynie

sinusoidalnie zmienny prąd elektryczny. Gęstość prądu g jest nierównomiernie rozłożona w przewodniku i określona przez następującą funkcję zespoloną zmiennej rzeczywistej rj:

g(g) = /lcosh(fc y/h7),

gdzie zł i A: są stałymi rzeczywistymi dodatnimi.

Wyznaczyć natężenie / prądu elektrycznego płynącego w przewodniku oraz jego moduł i fazę (p. W rozważaniach przyjmujemy jedną z dwóch wartości Vi, a mianowicie

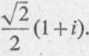
Rozwiązanie. Natężenie 7 prądu w przewodniku określa następująca całka:

b

I = a $g(n)dii,

0