00098490

270

in. FUNKCJE ZMIENNEJ ZESPOLONEJ

Ze wzoru (UJ.73) wynika, ie szereg potęgowy można wewnątrz koła zbicżnoici różniczkować wyraz po wyrazie.

Tw. (o zbieżności niemal jednostajnej). Szertg potęgowy jest jednostajni* zbieZny w każdym zbiorze domkniętym i ograniczonym, zawartym wewnątrz ko.‘a zbieinoid.

W szczególności, jeżeli szereg (UI.72) ma skończony promień zbieżności R, to szereg ten jest jednostajnie zbieżny w domkniftym kole o środku r₀ i promieniu OR, gdzie 6 jest dowolną liczbą z przedziału otwartego (0,1). W związku z tym mówimy, ie szereg (UI.72) jest w swym kole zbieżności niemal jednostajnie zbieżny.. Jeżeli R = +oo, to szereg potęgowy (III.72) jest jednostajnie zbieżny w domknię* tym kok o środku r₀ i dowolnym promieniu r.

Funkcje całkowite. Jeżeli szereg potęgowy (UI.72) ma promień zbieżności. R = +oo, a więc jeżeli jest to szereg zbieżny dla każdej wartości z, to jego suma jest funkcją określoną na całej płaszczyźnie otwartej. Funkcje takie mają ważne

Def. Funkcja całkowita jest to suma szeregu potęgowego zbieżnego na całej płaszczyźnie otwartej.

7. twierdzenia o holomorficzności sumy szeregu potęgowego wynika, że f u n cja całkowita jest holomorficzna na całej płaszczyźnie liczbowej. W dalszym toku wykładu zobaczymy. Że i na odwrót: każda funkcja holomorficzna na całej płaszczyźnie liczbowej jest funkcją całkowitą.

Rozważmy funkcję całkowitą

,(z-z₀)*

Jeżeli istnieje taka liczba n„. że dla każdego n ?>• n₀ mamy o, -■ 0, to funkcja całkowita jest wielomianem Jeżeli liczba n„ o wymienionej właściwości nie istnieje, a więc jeżeli szereg potęgowy, którego sumą jest funkcja /(z), ma nieskończenie wiele wyrazów różnych od rera (dla z * z₀). to/(2) nazywamy funkcją przestępną.

Pewne funkcje Całkowite, a więc sumy szeregów zbieżnych na całej płaszczyźnie mają takie właściwości, dzięki którym wygodnie się nimi posługiwać w wielu zagadnieniach. Dla funkcji tych wprowadzamy specjalne symbole i nazwy, często takie same, jakich używamy w analizie funkcji zmiennej rzeczywistej. Takie rozszerzenie znaczenia symbolu i nazwy musi być jednak tego rodzaju, żeby w przypadku, gdy zmienna zespolona przyjmuje wartość rzeczywistą, było odo zgodne ze z ustalonym dla rzeczywistych wartości argumentu.

Podamy teraz tego rodzaju rozszerzenie znaczenia nazw: funkcja wykładnicza przy podstawie ę, funkcja sinus i funkcja kosinus. Określamy mianowicie

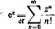
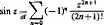
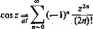
(111.74)

(111.75) oraz (IU.76)

Zauważmy, że dla rzeczywistych wartości * zmiennej z definicje te są identyczne ze znanymi rozwinięciami w szereg Maclaurina funkcji e\ sin* i cos*. Rozszerzenie znaczenia nazw i symboli tych trzech funkcji, dokonane za pomocą definicji (III.74)-(111.76), jest więc prawidłowe. Nawiązując do rozwinięć w szereg Maclaurina łatwo też udowodnić, że promienie zbieżności szeregów stanowiących prawe strony równości (III.74)—(111.76) są nieskończone. W tym celu wystarczy zauważyć, że kola zbieżności tych szeregów zawierają każdy punkt osi rzeczywistej, gdyż rozwinięcia' funkcji e*, sin* i cos* w szereg Maclaurina są zbieżne na całej osi liczbowej.

Z uwagi na określenie (ill.74), mamy dla urojonej wartości z —jy następujący związek

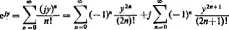
e'¹’ <= cosy+jsiny

czyli

(HL77)

a więc otrzymaliśmy znany skądinąd wzór Eulera.

Ponadto na podstawie schematu Cauchy'ego mnożenia szeregów mamy

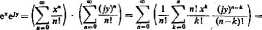
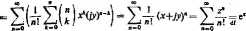
a więc jeżeli z = *+/K» to

(HŁ 78)

e» = _c*e''

Uwaga I. Jeżeli równość (UJ.77) oraz równość (UI.78), w których * iy są to liczby rzeczywiste, ag- x+ir. potraktować łącznic za definicję e*. to posługując się rozwinięciami funkcji siny, cosy i e* w szeregi MKlsurina oraz korzystając ze schematu Cmictiy'cgo mnożenia szeregów,