str104 (5)

104 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

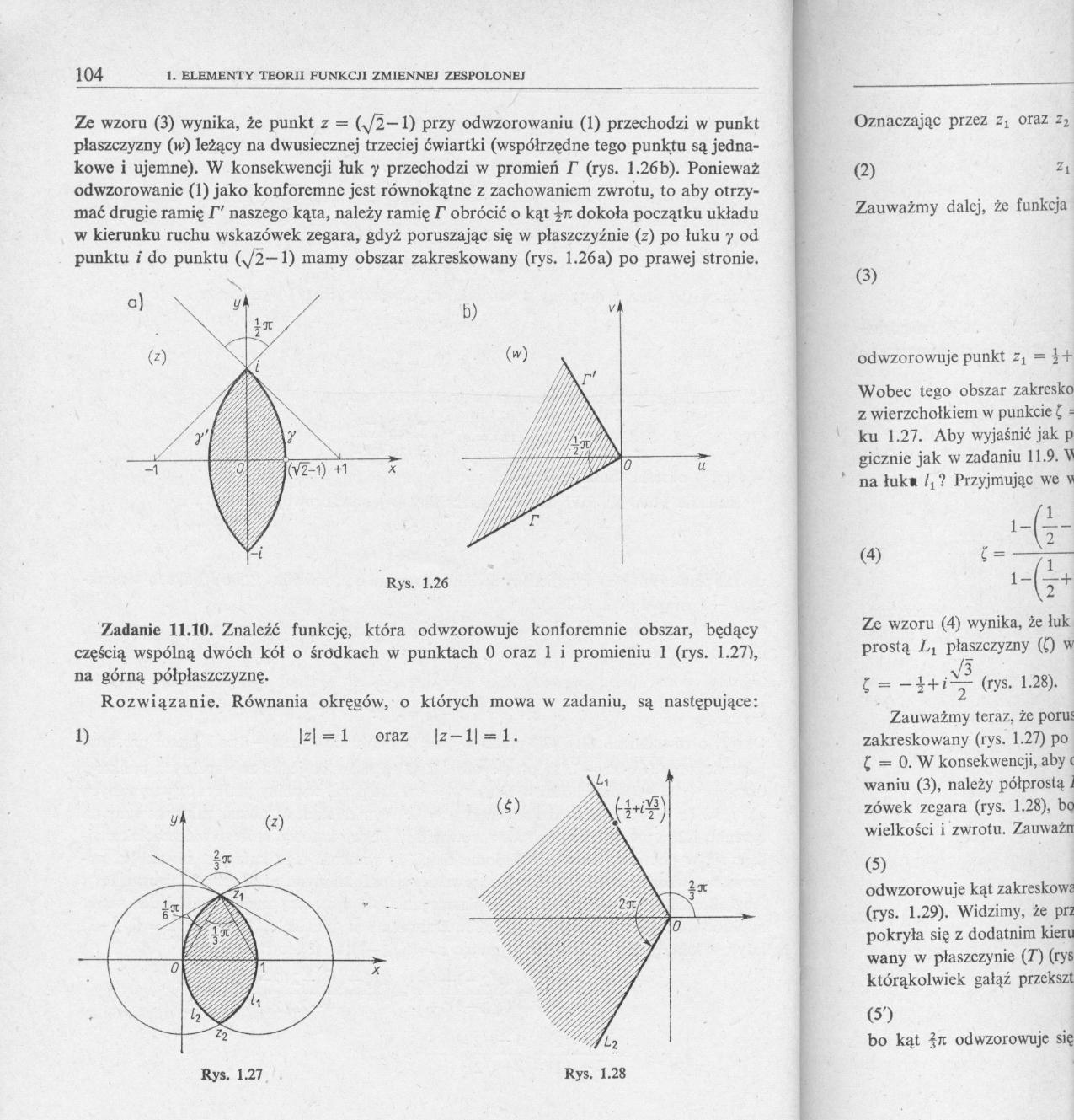
Ze wzoru (3) wynika, że punkt z = {-Jl— 1) przy odwzorowaniu (1) przechodzi w punkt płaszczyzny (w) leżący na dwusiecznej trzeciej ćwiartki (współrzędne tego punktu są jednakowe i ujemne). W konsekwencji luk y przechodzi w promień f (rys. 1.26b). Ponieważ odwzorowanie (1) jako konforemne jest równokątne z zachowaniem zwrotu, to aby otrzymać drugie ramię T' naszego kąta, należy ramię r obrócić o kąt dokoła początku układu w kierunku ruchu wskazówek zegara, gdyż poruszając się w płaszczyźnie (z) po luku y od punktu i do punktu (>/2—1) mamy obszar zakreskowany (rys. 1.26a) po prawej stronie.

X

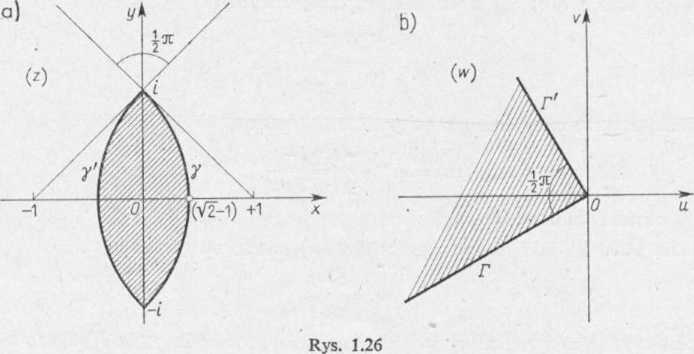
Zadanie 11.10. Znaleźć funkcję, która odwzorowuje konforemnie obszar, będący częścią wspólną dwóch kół o środkach w punktach 0 oraz 1 i promieniu 1 (rys. 1.27), na górną półpłaszczyznę.

Rozwiązanie. Równania okręgów, o których mowa w zadaniu, są następujące: 1)    |z| = 1 oraz |z —1| = 1.

Oznaczając przez z_x oraz z₂ (2)

Zauważmy dalej, że funkcja

(3)

odwzorowuje punkt z_x = £+

Wobec tego obszar zakresko z wierzchołkiem w punkcie £ = ku 1.27. Aby wyjaśnić jak p gicznie jak w zadaniu 11.9. V na łuk« /, ? Przyjmując we u

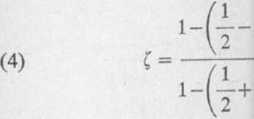
im

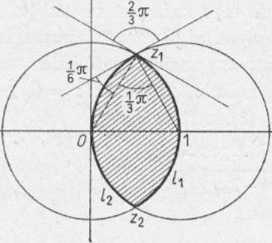
Rys. 1.27

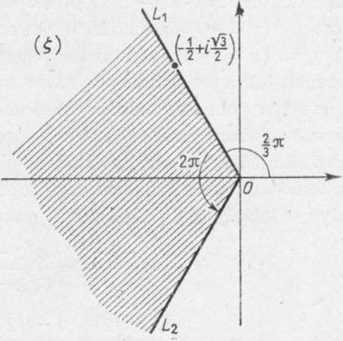
Ze wzoru (4) wynika, że łuk prostą L_x płaszczyzny (£) w v/3

£ = ^^rys‘ ^L28^

Zauważmy teraz, że porus zakreskowany (rys. 1.27) po £ = 0. W konsekwencji, aby ( waniu (3), należy półprostą 1 zówek zegara (rys. 1.28), bo wielkości i zwrotu. Zauważn

(5)

odwzorowuje kąt zakreskowa (rys. 1.29). Widzimy, że prz pokryła się z dodatnim kiera wany w płaszczynie (T) (rys którąkolwiek gałąź przekszt

(5')

bo kąt odwzorowuje się

Rys. 1.28