26695 str112 (5)

112 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

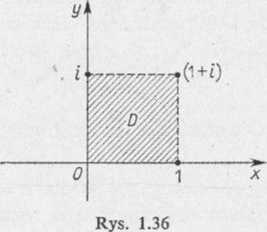
Łatwo zauważyć, że równania boków kwadratu D są następujące (rys. 1.36):

z = it, 0^/^ 1 z = i+t, 0 ^ t ^ 1 z=l + i'(l—t),    0</<l

z = t, O^Kl

(3)

—    równanie boku na osi Oy,

■— równanie boku równoległego do osi Ox,

—    równanie boku równoległego do osi Oy,

—    równanie boku na osi Ox.

Stąd kolejno

/[z(0] = z² = i²t² = -t² (4)

— na    boku    na osi Oy,

f[z(t)] — z²    =    (i+/)² =    (t²— l)+2it —na    boku    równoległym    do osi    Ox,

/[z(l)] = z²    =    2/(1 —/) +    2l(l —/)    —na    boku    równoległym    do osi    Oy,

/[z(0] = t²    — na    boku    na osi Ox.

Podstawiając związki (3) i (4) do wzoru (2), mamy

L = }| -2ti\ dt + } |(2/ + 2t)■ 11 dt+ } |(■-At + 2-20 (- i)\dt+ } |2/| dt,

ooo    o

L = \2tdt+ ^4t²+4dt+ $2\/4t²-4t + 5dt+ \2tdt,

OOO    o

L = 4|ldI + 2jVt² + l dt+2\\] At²—Ąt+5dt,

0    0    o

L = 2 [(l+^/2) +ln (1 + ^/2)] •

r

Zadanie 11.15. Wykazać, że funkcja G(z) = Log— jest funkcją Greena dla koła

M

|z|<r z biegunem w punkcie z₀ = 0.

Rozwiązanie. 1° Zauważmy przede wszystkim, że funkcja

G(z) = log

+y

(1)

jest harmoniczna i dodatnia w kole |z|<r z pominięciem punktu z₀ = 0, bo

r

Vx²+r

>1,