str072 (5)

I

72

1. elementy teorii funkcji zmiennej zespolonej

Rozwiązanie, a) Zauważmy, że

(1)

Z rozkładu tego widać, że funkcja po lewej stronie wzoru (1) ma wewnątrz konturu C zera

jednokrotne z_t = oraz z₂ = —Ąn. Wynika stąd natychmiast, że funkcja podcałkowa

ma w punktach z_l = \n oraz z₂ = — Ątc bieguny jednokrotne. Wobec tego, dla z

/(z) = , . , , zgodnie z twierdzeniem o residuach, mamy f sin *z

zdz

72

+ sinz

■>

Wyliczając znanym sposobem 1

(7)

Podstawiając równość (7) do v

(2)

Jp

sm^ ⁼ 2ni [^res-,/(z) + res_l2/(z)].

Obliczając residua funkcji podcałkowej /(z) kolejno w punktach zj oraz z₂, otrzymujemy odpowiednio

(3)    res .,/(z) = -\n,    res _Z2f(z) = -\n.

Podstawiając równości (3) do wzoru (2), mamy

zdz    ,

, —ry = 2tu‘(—Iji—Itt) = —ni. i —sin z

c

b) Zauważmy, że

(4)    (z²+l)² = (z-i)²(z + i)².

Z rozkładu tego widzimy, że lewa strona wzoru (4) jest funkcją mającą w punktach z_l = i

e^z

oraz z₂ = —i zera dwukrotne. Wynika stąd, że funkcja podcałkowa /(z) = ^ ²

ma w tych punktach bieguny dwukrotne. Aby rozstrzygnąć jak położone są bieguny z,

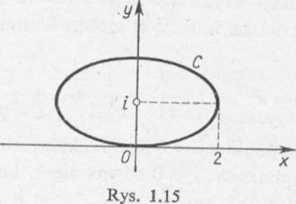
oraz z₂ względem konturu C, sprowadzamy równanie tego konturu do postaci (rys. 1.15):

2    --•>

Zadanie 10.3. Obliczyć całk

+ CO    +00

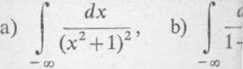
Rozwiązanie, a) Bierzem

(5)

(y-1)²

= 1.

(1)

która dla rzeczywistych warto

(2)

Stwierdzamy teraz, że funkcja funkcja R(z) określona wzorem każdy jest dwukrotny. Z tych t Biorąc powyższe pod uwagę i przypadku

(3)

Zgodnie ze wzorem (10.3), zas mamy

(4)    res_ZlR(z) = li:

Z równania (5) wnioskujemy, że tylko biegun z_Ł = i leży wewnątrz konturu C. W konsekwencji na mocy twierdzenia o residuach mamy

= li 2*

Podstawiając (4) do (3), mai

(6)

_l~₂dz = 2nires_Zlf(z).