74875 img235 (2)

10. Sygnały losowe 3.doc, 7/29

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH

funkcja S_x(co) została zdefiniowana dla pulsacji dodatnich i ujemnych, można również posługiwać się gęstością widmową mocy zdefiniowaną dla pulsacji fizycznych S_0X((o)

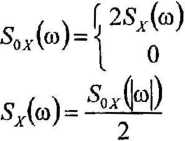
dla to > 0 dla to < 0

dla <og (~gc,oo)

iloczyn \/2nS_x((o)d(o przedstawia sobą część całej mocy sygnału zawartą w przedziale (co^co + do), całkowita średnia moc

10. Sygnały losowe 3.doc, 8/29

ZARYS TEORII SYGNAŁÓW STOCHASTYCZNYCH Twierdzenie Wienera-Chinczyna

Funkcja autokorelacji ^(x) sygnału stacjonarnego oraz gęstość widmowa mocy £(<») tego sygnału stanowią parę transformat Fouriera

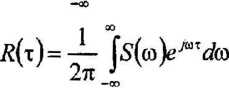
inne (rzeczywiste) postacie wyrażeń uwzględniając

e^J<az = cos to t + ysintoT S₀(co)=2S(co)