87500 Scan Pic0025

a zatem

Ico = 1 'od' , oraz	F = 41, stąd
s «§«*!	^1 f 1 .2 2 —o) =—ma co 4 ) 4

Rozwiązanie zadania 1.56 Prawidłowa odpowiedź: B.

F

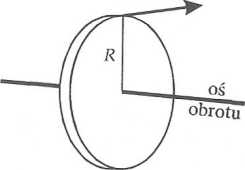
Moment siły M działając w czasie At na bryłę sztywną wykonującą ruch obrotowy zmienia moment pędu bryły o AL, przy czym MAf = At (często moment pędu oznaczany jest b ). W naszym zadaniu w chwili początkowej t = 0 moment siły i moment pędu są równe zeru: M = 0 i L = Ieo= 0. Po czasie t od rozpoczęcia ruchu zachodzi Mt = L.

Zatem dla pierwszego bloczka mamy: Lj = M,f, a dla drugiego bloczka L₂ = 2Mjt = 2L_V

Rozwiązanie zadania 1.57 Prawidłowa odpowiedź: A.

Wykonanie nad bryłą pracy Wpowoduje zwiększenie jej energii kinetycznej ruchu obrotowego dokładnie o wartość wykonanej pracy:

Wp Hi fi&f -f    i-hfiBł" fetUS -/?)■

Rozwiązanie zadania 1.58 Prawidłowa odpowiedź: C.

Początkowa energia potencjalna walca zmienia się podczas staczania w energię kinetyczną ruchu postępowego i obrotowego. Zgodnie z zasadą zachowania energii

1    1

mgh = —mu² +—Id)².

⁶ 2    2

Jeśli walec o promieniu r toczy się bez poślizgu, to prędkość liniowa punktów na jego obwodzie ma w każdej chwili taką samą wartość jak prędkość v tego walca w ruchu postępowym. Z drugiej strony między

prędkością liniową v punktów na obwodzie walca i jego prędkością kątową co istnieje związek v = cor. Tak więc

mgh = —mu² + —ij ^V

= — mu +

11    2 v²

WSpiS-raj' •—r- = 2 2    r²

1 2,1 2 3    2

= —mu +— mu wm-rtw .

2    4    4

stąd

Widzimy, że prędkość uzyskana przez środek walca u podstawy równi nie zależy ani od promienia, ani od masy walca. Momenty bezwładności innych brył, które mogłyby staczać się z równi (kule, rury itp.) są proporcjonalne do iloczynu masy i kwadratu promienia:

l-mr¹, (J^ = J-mr², J_rury =mr²), więc dla nich powyższy wniosek jest także słuszny.

Rozwiązanie zadania 1.59 Prawidłowa odpowiedź: A.

Ruch drgający harmoniczny to ruch odbywający się pod wpływem siły

F = -kx.

Wartość tej siły zmienia się wraz ze zmianą położenia x ciała, nie jest więc stała JF = const to warunek ruchu jednostajnie zmiennego). Ponadto siła F jest stale zwrócona do położenia równowagi. Jeśli więc ciało od tego położenia się oddala (O—>A, O—>B), to F jest siłą hamującą. Podczas zbliżania się do położenia równowagi (A—>0, B—»0) F jest siłą przyspieszającą. Tak więc ruch punktu od A do O jest ruchem niejednostajnie przyspieszonym.

Rozwiązanie zadania 1.60 Prawidłowa odpowiedź: D.

W zadaniu chodzi oczywiście o wartości prędkości i przyspieszenia. Jeśli położenie ciała drgającego ruchem harmonicznym wyrazić wzorem

x = Asineot,

to współrzędną x-ową (patrz objaśnienie do zad. 1.14) prędkości tego ciała przedstawia zależność (patrz [2], str. 73):

- 49 -