IMGX04 (3)

5 odróżniać elektron od pozostałych elektronów. Wynika z tego, że na każdym I orbitalu a mogą się znaleźć najwyżej dwa elektrony. Natomiast na każdym orbitali I n, S.... czyli na orbitalach X # 0 może się znaleźć do czterech elektronów, ponieważ I termy te są dwukrotnie zdegenerowane (patrz rys. 5.7 i 5.9).

W wypełnionych elektronami orbitalach wektory ż i wektory s są parami [I antyrównolegle, co daje wypadkowy wektor A = 0 i 5 = 0. Term molekularny jest [I więc termem '£* w liniowej molekule lub termem ^lA_t w wieloatomowej molekule j| nieliniowej. Inne termy występują wtedy, gdy orbitale nie są wypełnione. Jeżeli w molekule jest jeden elektron a, to A = 0, 5 = i i mamy term . Jeden elektron II n o wartościach A = 1 i 5 = ł daje term ²J7. Dwa nierównoważne elektrony a (np. [I 2pa i <rls na rys. 5.8), których A, = 0 i X₂ = 0, czyli A — 0, mogą mieć spiny [I równoległe, 5 = 1, lub antyrównolegle, 5 = 0, dają więc termy ³L* lub ^lZ*. Dwa 1 równoważne elektrony a (np. lstr i ols na rys. 5.8) wypełniają orbital i dają term [I ^lE*. Elektrony n i ó o liczbach X_t = 1 i A₂ = 2 dają A = 3, przy zgodnej orientacji j wektorów X, lub A = 1, przy przeciwnej orientacji wektorów X, przy czym ich spiny [I mogą być równoległe, 5=1, lub antyrównolegle, 5 = 0. Odpowiadające temu termy I to ³<P, ¹(p, ³n i ^ln. Każdy z tych termów ma inną energię.

Jeżeli dwa elektrony znajdą się na orbitalu dwukrotnie zdegenerowanym, to fj w kolejności energetycznej ich termów obowiązuje reguła Hunda, w myśl której [I najniższej energii odpowiada term o najwyższej multipletowości. Tak więc w przypa- i dku dwóch równoważnych elektronów n lub 5 występują termy i³Z*,z których | niższą energię ma term trypletowy ³Z*. Taką sytuację mamy np. w molekule tlenu i o konfiguracji elektronowej (<r_g ls)²{o_M ls)² (a_t2s)²(a_u2s)²(a_l2p)³(n_u2p)*(n_l2p)\ | gdzie ostatnie dwa elektrony n mają spiny niesparowane na najniższym poziomie | energetycznym, tzn. w stanie podstawowym, dlatego też molekuła tlenu jest I paramagnetyczna (por. punkt 8.1).

Tablica 5.1

Termy elektronów równoważnych

Konfiguracja ejektronów	Molekularne termy elektronowe
a
n	*n
5	^2 A ' |
m	M,
	‘z*. ^sz~. U
*»	li
a^4	•r*
V	^lz\^s£’,*r
6*	V.
5*	' Spl

Tablica 52 i

Termy elektronów nierównoważnych

Konfiguracja elektronów	Molekularne termy elektronowi
aa	^iZ*,^iZ*
on	*/7. ^s/7
ci	^lA,^lA
nn	'Z*,Z'.^1*.** 1
ni	*/J. >n, *<*►,
53	^xz\*z*>^lz~,*z‘j
	*z+,*z-,^1aSz-
***	WM$m.
tt*d	**Vf\‘*4 ^lr,^Ąi
it’0	^ln,^%n
ź** •	^iZ*,^lZ~,^lA,^iZ*,^lZ‘*A
n^96	^ln, *♦.

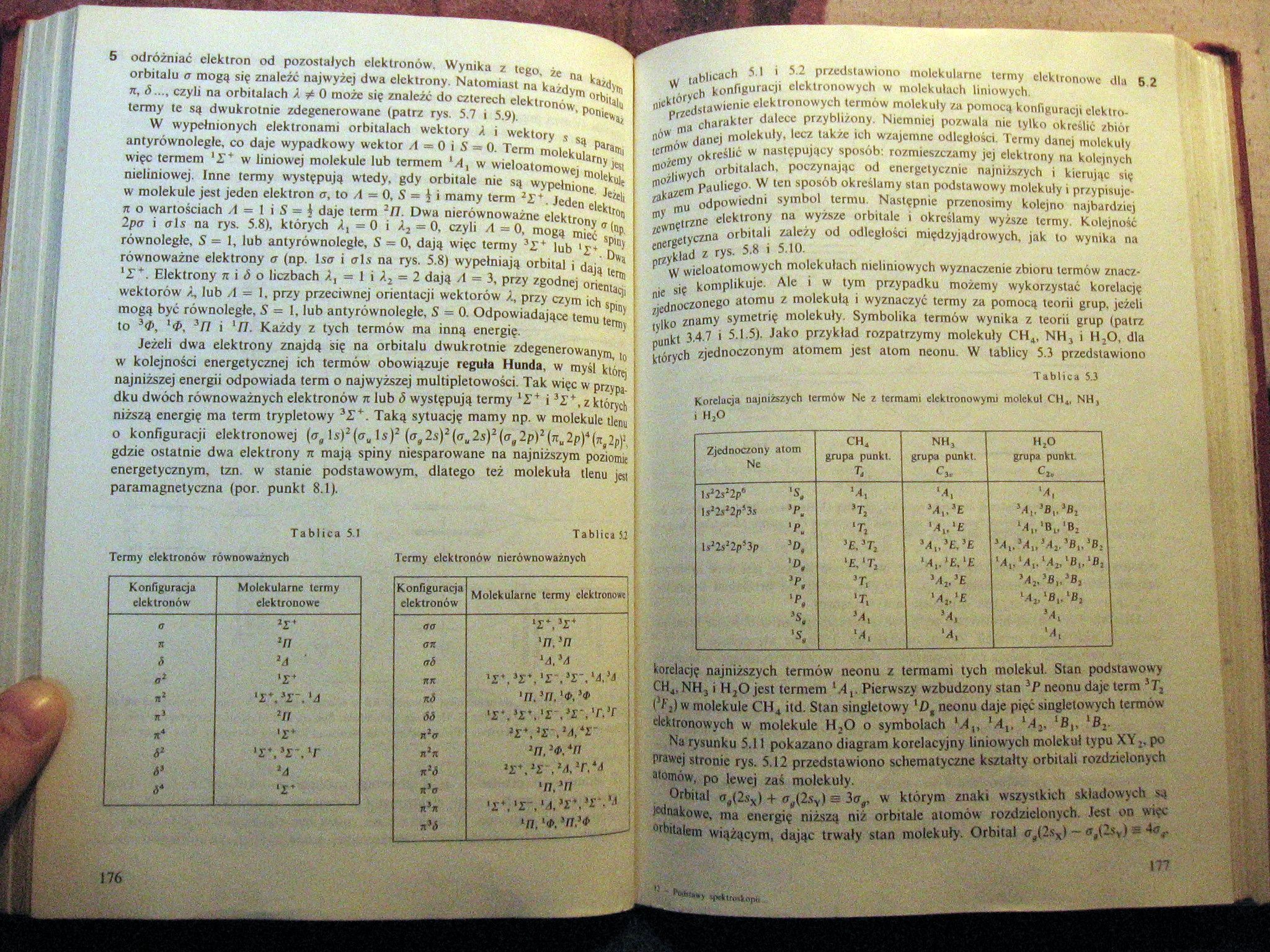
W tablicach 5.1 i 5.2 przedstawiono molekularne termy elektronowe dla 6.2 niektórych konfiguracji elektronowych w molekułach liniowych.

Przedstawienie elektronowych termów molekuły za pomocą konfiguracji elektro-nów ma charakter dalece przybliżony. Niemniej pozwala nie tylko określić zbiór termów danej molekuły, lecz także ich wzajemne odległości. Termy danej molekuły możemy określić w następujący sposób: rozmieszczamy jej elektrony na kolejnych możliwych orbitalach, poczynając od energetycznie najniższych i kierując się zakazem Paulicgo. W ten sposób określamy stan podstawowy molekuły i przypisujemy mu odpowiedni symbol termu. Następnie przenosimy kolejno najbardziej zewnętrzne elektrony na wyższe orbitale i określamy wyższe termy. Kolejność energetyczna orbitali zależy od odległości międzyjądrowych, jak to wynika na przykład z rys. 5.8 i 5.10.

W wieloatomowych molekułach nieliniowych wyznaczenie zbioru termów znacznie się komplikuje. Ale i w tym przypadku możemy wykorzystać korelację zjednoczonego atomu z molekułą i wyznaczyć termy za pomocą teorii grup. jeżeli tylko znamy symetrię molekuły. Symbolika termów wynika z teorii grup (patrz punkt 3.4.7 i 5.1.5). Jako przykład rozpatrzymy molekuły CH₄, NH₃ i H₂0, dla których zjednoczonym atomem jest atom neonu. W tablicy 5.3 przedstawiono

Tablica U

Korelacja najniższych termów Ne z termami elektronowymi molekuł.CH*. NHj i HjO

Zjednoczony atom Ne	ch4 grupa punkt. V	NHj grupa punkt. Cu	HjO grupa punkt Cu
1®lip! >s.	^ł4,		'Ax
ls*2»*2^3s ^iP,	M ||	M„*E	^3At ,^}Bv^3B2
^lP„	‘T?	lipi	^l4„ ‘By 'Bj
li^12s^J2p^53p ^3Dt	^3E, ^3Tj
%:	'£, ‘Tj	^lA„^lE, '£	Mz, pili
^3P,	^3T,	M*.^3£	.Mi
mś	s
	%	%	^3 At
g	M,	*4,.	'Ay |

korelację najniższych termów neonu z termami tycb molekuł. Stan podstawowy Ctt₄, NH₃ i HjO jest termem M,. Pierwszy wzbudzony stan ³P neonu daje term ^sT_ł rajL) w molekule CH₄ itd. Stan singletowy neonu daje pięć singletowych termów elektronowych w molekule H₂0 o symbolach M_łt ^lA_v ^lĄ₂, ^lB_t, ⁱB_x.

Na rysunku 5.1 i pokaźno diagram korelacyjny liniowych molekuł typu XY po prawej stronie rys. 5,12 przedstawiono schematyczne kształty orbitali roztbdelpnych atomów, po lewej zaś molekuły.

Orbita! o_tf(2%) + a_fl(2%) s 3o_t, w którym znaki wszystkich składowych są jednakowe, ma energię niższą niż orbitale atomów rozdzielonych. Jest on więc orbitalem wiążącymi dając trwały stan molekuły. Orbita! <r,(2s_x) ~ <r,(2s_v) « 4$^.

m

W -    spiklroikopfi ..