230 (48)

466 Dodatki

b)    w płaszczyźnie prostopadłej do osi rury ciecz jest idealnie zmieszana, zatem prędkość i temperaturę cząstek cieczy można w tej płaszczyźnie uśrednić,

c)    pojemności cieplne i gęstości płynów oraz ścianki w zakresie rozpatrywanych temperatur są stałe,

d)    współczynniki przenikania ciepła są równe we wszystkich punktach powierzchni wymiany ciepła,

e)    straty ciepła do otoczenia są pomijałnie małe,

f)    przekrój poprzeczny rury i charakter przepływu (laminamy, turbulentny) są niezmienne,

g)    pojemność cieplna warstwy skroplin jest pomijalna (można ją uwzględnić dodając do pojemności cieplnej ścianki).

Bilans energetyczny strumienia cieczy dla pojedynczej rury o długości dl jest następujący:

SiyCi — dl+ 0'ci-— dl=    tf)dl

ot    dl

lub

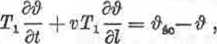
(B.16)

gdzie

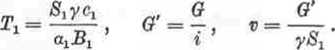
Bilans cieplny ścianki jest następujący:

Bdyto^eto    —a₂B₂(ó_p—i?so)dl—eh

lub

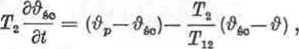
(B.18)

gdzie

rr _    _m Bgyrfta T_a a_tB_l

²    o*!?, ’    ¹² _aiB> ’ T_u a,B_t'

Transformując równania (B.16) i (B.18) otrzymamy

(B.19)

T₁s^{s) + vT_J — — = O^s)— ■&($), d l

Zmienne &(s) i 0_tc(s) w tych równaniach oznaczają transformaty odchyleń temperatury od wartości nominalnych w każdym punkcie wzdłuż wymiennika. Po-wyeliminowaniu #*,(«) uzyskamy równanie

rdtf(s)    b

--57-+■*(») =    (B.21)

<1 cU    a

gdzie

(r_l«+i)(T₁₁r_!,«+r,_t+T_ł)-2^,1

TAT„T_tt+X_m+TJ

b    1

u^_ T_lT,s² +(T_l+T₂+T₁ TJT_n)s +1'

Rozwiązanie równania (B.21) dla warunków początkowych (i? = 0, Z = 0) ma-postać

m

&p(s)

= - (l-e-⁰"”)

(B.22)-

lub oznaczając czas przepływni płynu przez rurę ljv = r (opóźnienie transportowe) otrzymujemy

dj>(s)

= -(1-6—) a

(B.23)-

Wyrażenie bja można rozłożyć na czynniki, aby otrzymać równoważne stałe-czasowe T' i T", ułatwiające określenie charakterystyki częstotliwościowej. Ponieważ wyrażenie określające a ma w liczniku s^a, a w mianowniku s, zatem (1—e~“') wykazuje stałe oscylacje amplitudy i przesunięcia fazowego w zależności od częstotliwości. Powoduje to występowanie maksimów rezonansowych w^r -wykresie pełnej charakterystyki częstotliwościowej. Zjawiska rezonansowe wystąpiły w niektórych badaniach doświadczalnych [6], trudno jest je natomiast zaobserwować, jeżeli temperatura wyjściowa ogrzewanego medium jest zbliżona do temperatury pary, gdyż wówczas amplituda oscylacji jest bardzo mała.

Przykład liczbowy. Określić transmitancję i?(s)/i?_p(s) wymiennika ogrzewanego parą wodną.

Dane: rury miedziane o długości l = 2,4 m, u = 9,5 mm, g = 1,0 mm. Dla jednej rury: 2^= 0,0534 01, 21, = 0,0598 m, = 0,000227 m¹, Bgy^ = = 0,533 kG/rn, c_it = 0,094 kcal/kG °0.

Prędkość wody

v = 0,3 m/s .

Średnia temperatura wody

Ci = 1,0 kcal/kG °C .

dsr= 66°C ,

w    ⁹