233 (30)

448 9. Spektroskopia laserowa

448 9. Spektroskopia laserowa

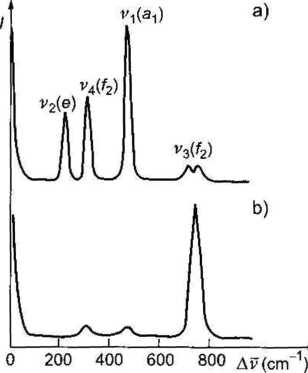
Rys. 9.6. Porównanie widm: a) Ray-leigha i Ramana; b) hiper Rayleigha i hiper Ramana CCl.i cieczy (No--Linear Raman Spectroscopy and its Chemical Applications, red. W. Kie-fer, D. A. Long, D. Reidel, Dordrecht 1982)

Naświetlając układ silnym światłem lasera o częstości można obserwować światło rozproszone o częstościach 2Fq ± Frr, gdzie Frr jest częstością hiperramanowską. Składowe hiperramanowskie są na ogół dobrze odseparowane od składowych ramanowskich. Składowa o częstości 2Fo nazywa się częstością hiper Rayleigha. W przeciwieństwie do składowej Rayleigha, nie pojawia się ona zawsze, a tylko wówczas, gdy cząsteczka rozpraszająca nie ma środka symetrii. Widmo hiper Ramana obserwować można dla gazów, cieczy i ciał stałych.

Aby zrozumieć pojawienie się składowej hiper Ramana przypomnijmy zależność indukowanego momentu dipolowego od natężenia pola elektrycznego (równanie (1.127))

A^ind ⁼ p^ + p^ “I^- pf^ ⁼ cne -f-1/2dcc 4- l/6^y€€€ 4~ ... (9.6)

gdzie: (3 - hiperpolaryzowalność, 7 - druga hiperpolaryzowałność. Są to tensory rzędu, odpowiednio 3. i 4. Jednostką hiperpolaryzowalności jest CV^-2 nr³, zaś jednostką 7 - CV~³ m⁴. O ile typowe wartości polaryzowalności są rzędu 10 ⁴⁰ CW'¹ m², to /Sjest 10^_5° CV~² m³, a 7 - rzędu 10^-61 CV“³ m⁴.

Jeżeli przyjąć e = eosin27TŁ/o^ to

Otrzymujemy więc z członu drugiego rzędu //²⁾ rozproszenie świa-:ła z podwojoną częstością w stosunku do częstości światła padającego. Jest to tzw. druga harmoniczna. Znamy wiele materiałów, na przykład kryształy KB^Os, KPB, które wykorzystuje się do dublowania częstości .

A jakie znaczenie w tym procesie ma hiperpolaryzowalność? Podobnie, jak w przypadku polaryzowalności, nie znamy zależności Q od współrzędnych normalnych Q. Możemy rozwinąć ją w szereg Maclaurina

3 A'-6 , o n s

m) = 0o+ E (Wa) Q + ~    (⁹-⁸>

i=1    \^a(*'Q=Q

Jeżeli na cząsteczkę pada wiązka laserowa o częstości uo, a drganie normalne Q ma postać Qi — Qw cos 2v_tt, to podstawiając to wyrażenie oraz rozwinięcie Taylora do (9.8) otrzymujemy układ

$0^0 COS 47T^o£

Ten człon odpowiada za składową rozproszenia hiper Rayleigha. Uwzględnienie następnych członów w rozwinięciu (9.6) prowadzi do członów

(00/dQi)Q₀QQf.o{cos(4^o ± Vi)t)

odpowiedzialnych za składowe rozproszenia hiper Ramana.

Aby zaobserwować to trójfotonowe zjawisko, potrzebne są wiązki laserowe dużej mocy ze względu na małe wartości pochodnej hiperpo-laryzowalnośei po współrzędnej normalnej (<9#/<9Q*)q=o> które muszą być różne od zera. Schemat poziomów energetycznych przedstawiony jest na rysunku 9.4d. Jak można się domyśleć, obowiązują inne reguły wyboru dla rozproszenia hiper Ramana niż dla zwykłego (liniowego) rozproszenia Ramana. Ogólnie możemy zapisać

r{M ® r(fi_ijk) 0 r($&) = Ai    (9.9)

gdzie 'ip_v' jest funkcją falową stanu wyższego, a U'v" jest funkcją falową stanu niższego oscylacyjnego. Zbiór wskaźników i, j, k to x, y, z, a symbol A\ oznacza reprezentację pełnosymetryczną. Jeżeli stanem początkowym jest stan o liczbie kwantowej v — 0, czyli i~'('j/V') = A), to otrzymujemy regułę r(?/v) = r(6_t]k). Określenie symetrii składowych tensora hiperpolaryzowalności nie jest takie proste, tensor ten ma bo-