25a (11)

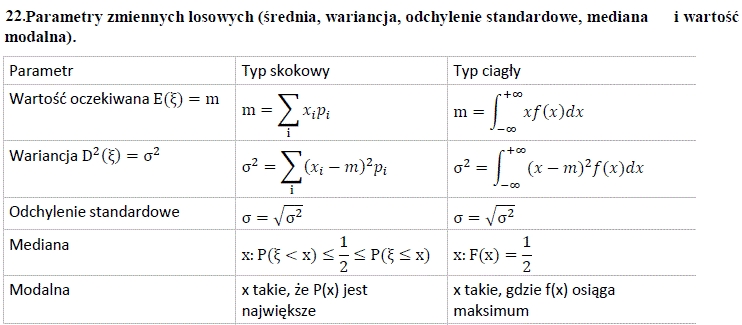
22.Parametry zmiennych losowych (średnia, wariancja, odchylenie standardowe, mediana i wartość modalna).

Parametr	Typ skokowy	Typ ciągły
Wartość oczekiwana E(2j) = m	^m = 'YJ^xiPi	r + CO m = 1 xf(x)dx co
Wariancja D^2(ę) = o^2	o^2 = - m)^2Pt i	r+ co o^2 = (x - m)^2f(x)dx J — CO
Odchylenie standardowe	o = y o^2	o = y a^2
Mediana	x: P(? < x) < ^ < Pg < x)	x=F(x)=i
Modalna	x takie, że P(x) jest największe	x takie, gdzie f(x) osiąga maksimum