5378219166

11

WYKŁAD i. PODSTAWY RACHUNKU PRAWDOPODOBIEŃSTWA

1.3. Parametry zmiennych losowych

Kwantylem rzędu p, p e (0,1) rozkładu zmiennej losowej X nazywamy liczbę £_p spełniającą nierówności

(1.3.1)

p(x^<r_P)^p,

p(x^_p)^i-p.

Nierówności (1.3.1) nie wyznaczają kwantyli jednoznacznie. Gdy dystrybuanta F (x) jest ciągła, to kwantyl £_p jest rozwiązaniem równania F(x) = p. Rozwiązanie to też nie musi być jednoznaczne.

Mediana oznaczana symbolem Me jest kwantylem rzędu p = 1/2, czyli Me = £1/2. Kwantyle rzędów p = 1/4 i p = 3/4 nazywa się kwartylami rzędu 1 i 3 i oznacza Qi i (>3, czyli Qi = £1/4 i Q$ = £3/4. Mediana jest kwartylem rzędu 2: Qg = £2/4 = Me. Do wskaźników rozrzutu zmiennej losowej zalicza się odchylenie ćwiartkowe Q = (£3/4 - ^m)l2.

Wartość oczekiwana EX zmiennej losowej X (zwana również średnią teoretyczną) jest określona osobno dla zmiennych skokowych, a osobno dla zmiennych typu ciągłego. Dla zmiennych skokowych jest to wzór

EX = xtpi + x₂p₂ + • • • = £>p_fc ,    (1.3.2)

k

a dla zmiennych losowych typu ciągłego - wzór

(1-3-3)

EX = J xf(x)dx.

Gdy chcemy obliczyć wartości oczekiwane potęg zmiennych losowych, to wzory (1.3.2) i (1.3.3) przybierają postać odpowiednio

EX" = ifpi + x£ P2 + ■ ■ ■ = 53 ijjp,    (1.3.4)

k

oraz

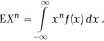
(1.3.5)

Ważnym parametrem zmiennej losowej X jest wariancja teoretyczna D²X określona wzorem

D²X - E{X - EX)² - EX² - (EX)²    (1.3.6)

oraz odchylenie standardowe O określone wzorem

u = y^D²!.

Odchylenie standardowe nazywane jest również dyspersją.

Uwaga. Wariancja D²X jest również często oznaczana przez V(X) lub Var(X).

Przykład 1.3.1. Niech zmienne losowe X i Y będą takie, jak w przykładzie 1.2.1. Ponieważ P (X = —1) = P (Y = —1) = 1/2 oraz P (X = 1) = P (Y = 1) = 1/2, zmienne X i Y mają ten sam rozkład, mimo że są różne: X = -Y. Wobec tego mają te same parametry, wartość oczekiwaną określoną wzorem (1.3.2) i wariancję określoną wzorem (1.3.6), gdzie EX² obliczamy ze wzoru (1.3.4).

D²X = D²Y = 1.

Medianą Me = £1/2 jest dowolna liczba -1 $ £1/2 $; 1. Można więc przyjąć £1/2 = 0, ale można też przyjąć £1/2 = -1 lub <;i/2 = 1. Widać, że w tym przypadku mediana nie jest pożytecznym parametrem.