029

29

2.1. Rozkłady i parametry zmiennych losowych

e)    Pr(0.25<X< 1.25) = F(1.25)-F(0.25) = 0.28125-0.0078125 =0.273437,

f)    Pr(l <X<2) = F(2)-F(l)-Pr(X = l)+Pr(X = 2)

= 0.75 - 0.125 - 0.125 + 0.25 = 0.75.

Przykład 2.1.3.

Dla zmiennej losowej X o dystrybuancie F(x) z przykładu 2.1.2, obliczyć kwantyle rzędu p G (0,1). Jako szczególny przypadek rozpatrzyć kwartyle, w tym medianę.

Rozwiązanie.

Ponieważ dystrybuanta F(x) jest nieciągła (patrz rysunek 4), to rozważymy następujące

przypadki:

a)    p 6(0,0.125],

b)    p e (0.125,0.25],

c)    p e (0.25,0.75],

d)    pe (0.75,1).

Jeżeli dla p € (0,1) istnieje x takie, że F(x) = p, to x jest kwantylem Ę_p rzędu p, tzn. nierówności Pr(X < ł;_p) > p i Pr(X > t;_p) > 1 — p są równoważne równaniu F(Ł,_P) = p. Zatem dla p 6 (0,0.125) kwantyl Ę_p rzędu p wyznaczamy z równania Ę,_p/% = p dla (j_p € (0,1], czyli Ę,_p = 2\/2p. Analogicznie dla p e (0.25,0.75] kwantyl £,_p rzędu p jest rozwiązaniem równania Z,²/2 — Ł,_p + 0.75 = p dla ^_p e (1,2], czyli £ = (2 + y/^p — 2) /2. W przypadkach b) i d) nie istnieje takie x, aby zachodziła równość F(x) = p. Dla p e (0.125,0.25] kwantylem jest liczba Ę_p = 1, bo Pr (A < 1) = F(l) +Pr(X = 1) = 0.25 ^ p oraz Pr(X ^ 1) = 1 —Pr(X < 1) = 1 — F(l) = 0.875 > p. Analogicznie dla p € (0.75,1) kwantylem jest łż,_p = 2.

•    Kwartylem rzędu pierwszego jest = 1.

• Kwartylem rzędu drugiego jest <^₂ = (2 + 2\/2)/2    1.70711.

•    Kwartylem rzędu trzeciego jest <^₄ = 2.

Mediana jest kwartylem rzędu drugiego.

Przykład 2.1.4.

Dla zmiennej losowej X o dystrybuancie F(x) z przykładu 2.1.2, obliczyć EX i D²X. Rozwiązanie.

Wartość oczekiwana zmiennej losowej X wyraża się wzorem

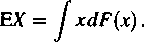
Pochodna F'{x) nie istnieje w punktach x=l i x = 2. Ponieważ w pozostałych punktach