52301 img006ô4

ROZKŁAD PO!SSON'A
Drugim wa┼╝nym rozk┼éadem teoretycznym zmiennych losowych dyskretnych jest rozk┼éad Poisson'─ů, zwany te┼╝ rozk┼éadem zdarze┼ä rzadkich b─ůd┼║ prawem ma┼éych liczb. Znajduje zastosowanie wsz─Ödzie tam, gdzie obserwuje si─Ö du┼╝─ů liczb─Ö zdarze┼ä, a prawdopodobie┼ästwo sukcesu jest ma┼ée. Wyst─Öpuje on jako przybli┼╝enie rozk┼éadu dwumianowego przy spe┼énieniu dw├│ch warunk├│w: a) liczba do┼Ťwiadcze┼ä powinna by─ç wystarczaj─ůco du┼╝a (praktycznie n > 100);
b) stałe prawdopodobieństwo powinno być bliskie zeru (praktycznie p < 0.1).
Zastosowania praktyczne rozk┼éadu Poisson'a s─ů rozliczne i np rozk┼éad ten mo┼╝e by─ç u┼╝yty by charakteryzowa─ç takie zjawiska, jak liczb─Ö brak├│w' w produkowanych urz─ůdzeniach, liczb─Ö awarii, liczb─Ö nieszcz─Ö┼Ťliwych wypadk├│w w pewnym przedziale czasow'ym itp Rozk┼éad Poisson'a jest okre┼Ťlony wzorem:
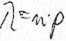
Xk .
P(X = k) = -e
Podstawowe parametry rozkładu:
E(X) = X; D2(X) =X:
4x
y>=~T'
i
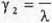
Warto┼Ť─ç oczekiwana Wariancja
Współczynnik asymetrii Współczynnik spłaszczenia
ZADANIE 5

Fabryka produkuje żarówki. Prawdopodobieństwo wyprodukowania żarówki wadliwej wynosi 0.002. Jakie jest prawdopodobieństwo, że w wyprodukowanej partii 1000 żarówek znajdzie się:
1) nie wi─Öcej ni┼╝ 5 ┼╝ar├│wek wadliwych,
2) 5 ┼╝ar├│wek wadliwych.
Oblicz podstawowe parametry statystyczne rozkła
>£Ó p-O/GOl
ZADANIE 6
Podręcznik wydano w nakładzie 100000 egzemplarzy. Prawdopodobieństwo tego, że podręcznik zostanie źle oprawiony, jest równe p = 0.0001.
Znale┼║─ç prawdopodobie┼ästwo tego, ┼╝e w nak┼éadzie pojawi si─Ö 5 ┼║le oprawionych ksi─ů┼╝ek. . \
Centrala telefoniczna zak┼éadu obs┼éuguje 100 abonent├│w. Prawdopodobie┼ästwo tego, ┼╝e w ci─ůgu jednej minuty abonent zadzwoni do centrali, jest p = 0.01. Znale┼║─ç prawdopodobie┼ästwo tego, ┼╝e w ci─ůgu jednej minuty zadzwoni:
a) dokładnie trzech abonentów; )

c) wi─Öcej ni┼╝ trzech abonent├│w;
d) co najmniej jeden abonent.
b) mniej ni┼╝ trzech abonent├│w; p ┬╗
ZADANIE 8
Tkaczka obsługuje 1000 wrzecion. Prawdopodobieństwo zerwania się nici na jednym wrzecionie w czasie jednej minuty Jest równe 0.003.
Znale┼║─ç prawdopodobie┼ästwo tego, ' ' : jednej minuty zerw─ů si─Ö:
a) dwie nici;
b) mniej ni┼╝ dwie nici,
c) wi─Öcej ni┼╝ dwie nici;
d) co najmniej jedna ni─ç.
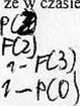
Wyszukiwarka
Podobne podstrony:
55156 statystyka matematyczna cw3b ROZKŁAD POISSON A Drugim ważnym rozkładem teoretycznym zmiennych
20 WYK┼üAD 2. ROZK┼üADY ZMIENNYCH LOSOWYCH Je┼Ťli n jest du┼╝e, to ÔÇöjest bliskie jedynki, a wi─Öc s2 i S2
statystyka matematyczna cw3a STATYSTEMATYCZNA ROZK┼üAD BERNOULLI EGO Rozk┼éad dwumianowy, dotycz─ůcy zm
77114 statystyka matematyczna cw3a STATYSTEMATYCZNA ROZKŁAD BERNOULLI EGO Rozkład dwumianowy, dotycz
DSCF1018 Drugim wa┼╝nym rozk┼éadem z pr├│by jest rozk┼éad!Przyjmuj─ůc, ┼║┬ž zmienna X ma ┼Ťredni─ů f odch. st
DSCF1019 Drugim wa┼╝nym rozk┼éadem z pr├│by jest rozk┼éad J ┼Ťrednie) arytmetycznej. Przyjmuj─ůc, ┼╝e zmien
statystyka skrypt�27 Br Po naci┼Ťni─Öciu przycisku tZmiennal wskazuje si─Ö zmienn─ů, do kt├│rej ma by─ç do
IMAG0569 ┼ütemieniaFulbe lub Mandingo. Kronika ta obejmuje okres ÔÇ×od po-┼ü- do 1656 r. Drugim wa┼╝nym d
img006 (68) po cz─Ö┼Ťci socjologiczna nad tymi zagadnieniami podejmowana jest przez pryzmat badania sp
statystyka 2 7 STATYSTYKA MATEMATYCZNAZmienne losowe ZMIENNA LOSOWA DYSKRETNA Z Rozkładem imiennej l
img318 £/>*= 1 ft Rozkład zmiennej losowej dyskretnej może być zadany za pomocy tabeli, analitycz
Wykład 2Rozkłady zmiennych losowych2.1. Rozkłady dyskretneRozkład dwupunkłowy Zmienna losowa X ma
wi─Öcej podobnych podstron