266 267 (12)

266

Rozdział 9. Determinanty dochodu narodowego. Analiza krótkookresowa

267

Czfti III. Podstaw; makroekonomii

Są na nim proste ilustrujące funkcje oszczędności i inwestycji, których kształt odpowiada danym liczbowym zawartym w tablicy 9.2. Proste te przecinają się w punkcie E przy Y = 100. W punkcie tym planowane inwestycje są równe piano, wanym oszczędnościom, a więc występuje stan równowagi. Należy podkreślić. ż_c osiągnięcie takiego stanu w gospodarce nic jest wcale proste. Bowiem nie tylko nieco inne podmioty inwestują, a inne oszczędzają, ale ponadto decyzje inwestycyjne zależą od innych czynników niż decyzje o oszczędzaniu. Stąd też możliwe są sytuacje, w których suma planowanych inwestycji jest różna od sumy planowa-nych oszczędności. Załóżmy, żc I>S. Oznacza to, że łączne planowane wydatki inwestycyjne i konsumpcyjne są większe od wytworzonej produkcji (na rys. 9.9 sytuację taką mamy przy Y = 80). Powstała nadwyżka popytu prowadziłaby do wzrostu produkcji i dochodu narodowego, co zwiększałoby poziom oszczędności aż do zrównania ich z inwestycjami. Gdyby zaś planowane inwestycje były mniejsze od planowanych oszczędności (na rys. 9.9 przy Y = 120). to powstała nadwyżka podaży towarów wymusiłaby zmniejszenie produkcji i dochodu narodowego. Przy danych funkcjach planowanych inwestycji i planowanych oszczędności istnieje więc tylko jeden poziom dochodu narodowego zapewniający równowagę (w naszym przykładzie poziom ten wynosi 100).

9.5. Mnożnik

W poprzednim punkcie rozważaliśmy, jak wyznacza się poziom dochodu narodowego w stanie równowagi przy danej konkretnej funkcji agregatowego popytu. Teraz zastanowimy się nad pytaniem, jak przesunięcie tej funkcji wpływa na dochód narodowy w stanic równowagi.

Jak wiemy z wcześniejszych rozważań, położenie funkcji agregatowego popytu w układzie współrzędnych zależy od jej nachylenia, określonego przez wysokość krańcowej skłonności do konsumpcji, oraz od poziomu wydatków autonomicznych (rys. 9.8). Załóżmy, żc następuje zmiana wydatków autonomicznych, oznaczająca przesunięcie funkcji agregatowego popytu. Przyjmijmy, żc zmiana tych wydatków dokonuje się w wyniku zmiany wydatków inwestycyjnych. Powstaje pytanie, jak zmiana autonomicznych wydatków inwestycyjnych oddziałuje na wielkość dochodu narodowego w stanie równowagi. Rozważmy tę kwestię, wykorzystując wcześniejszy przykład liczbowy (tablica 9.2).

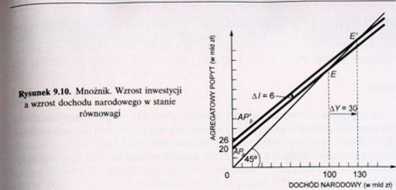
Załóżmy, żc początkowo gospodarka znajduje się w stanic równowagi przy P= 100 mld zł (punkt E na rys. 9.10). Załóżmy ponadto, żc w rezultacie optymistycznych nastrojów przedsiębiorców następuje zwiększenie wydatków inwestycyjnych

0    6 mld zł (dalej pomijamy miliardy i złote). Mamy więc A/ = 6. Na rysunku 9.10 prosta AP_r przesuwa się do położenia AP'. W tej sytuacji na rynku towarów pojawia się nierównowaga, gdyż Y = 100, zaś AP ’ = 106. Mamy więc AP;>Y. Wiemy z wcześniejszych rozważali, że przy powstaniu nadwyżki popytu następuje wzrost produkcji

1    dochodu narodowego. Powstaje jednakże pytanie, o ile wzrośnie dochód narodowy?

Początkowy wyrost wydatków inwestycyjnych o 6 powoduje wyrost produkcji dóbr inwestycyjnych w celu zaspokojenia tego dodatkowego popytu. Rozważamy gospodarkę w warunkach niepełnego wykorzystania zdolności wytwórczych, więc wzrost produkcji jest możliwy poprzez pełniejsze wykorzystanie istniejących zdolności wytwórczych. Dzięki produkcji i sprzedaży dodatkowych dóbr inwestycyjnych powstają dodatkowe dochody (AV = 6). które trafiają do gospodarstw domowych. Na tym proces jednakże się nic kończy. Gospodarstwa domowe przeznaczają część dodatkowych dochodów na zakupy dóbr konsumpcyjnych. Rozmiar dodatkowych wydatków konsumpcyjnych zależy od wysokości krańcowej skłonności do konsumpcji (ik,_k). Im k,_k wyższe, tym większy przyrost popytu konsumpcyjnego (AC'). W naszym przykładzie *„ = 0.8 więc AC' = 0.8 6 = 4.8. Dodatkowy popyt konsumpcyjny powoduje wzrost produkcji dóbr konsumpcyjnych i wyrost dochodu o 4.8. Ten wzrost dochodu pociąga za sobą dalszy wzrost popytu konsumpcyjnego, równy AC = 0.8 • 4.8 = 3.84 (wv.rost popytu konsumpcy jnego można też obliczyć z formuły AC *= 0,8^; - 6 = 3,84). Procesy kumulacyjne przyrostu popytu i dochodu zachodzą nadal, ale już w tym momencie analizy łatwo zauważyć, że pierwotny przyrost wydatków inwestycyjnych (A/ = 6) powoduje znacznie większy przyrost dochodu _ narodowego (do tego momentu AV = 6 + 4,8 + 3.84 = 14,64. a przecież proces ku*

Ij mulacyjny nie jest zakończony). Warto zauważyć, że pierwotny przyrost wydatków inwestycyjnych zapoczątkował łańcuch wtórnych wydatków konsumpcyjnych. Tworzą one pewien malejący ciąg geometryczny, którego początkowe wyrazy są następujące: 6: 0.8 • 6; 0,8^: • 6:0.8' ■ 6 itd. Matematycy znaleźli wzór na sumę wyrazów

takiego ciągu, który zastosowany do naszego przykładu ma postać: j _Qg' ^ ⁼

Suma ta wskazuje właśnie na łączny przyrost dochodu narodowego wynikający W z pierwotnego wzrostu wydatków inwestycyjnych o 6. Stąd:

&Ym '    .4/.    (9.24)

1 -JfcjA