26 (468)

50

Rozwiązanie

Uwolniona od więzów (lin) belka jest pokazana na rys. I.39b. Siiy oddziaływania lin R_A i R_Q sę skierowane wzdłuż lin (a więc pionowo w górę), a wartości tych sił są równe szukanym siłom napięcia lin. Określimy je z warunków równowagi płaskiego układu sił.Ze względu na równoległość wszystkich sił możemy wykorzystać tylko dwa równania równowagi, a mianowicie sumę rzutów na oś pionową oraz sumę momentów względem dowolnego punktu. Wyglądają one następująco:

£^piy - R_A - Q - G * R_e = 0.

£m_1a

' ł

Po rozwiązaniu tego układu otrzymujemy

Rq ^s y 0. ♦ y G = 2600 N,

R_a ■ya*|G « 4600 N.

1.2.2. Oednorodna pozioma belka AB (rys. I.40a) o ciężarze G * 800 N i długości 1 « 3 m została końcem A zamocowana na stałej podporze przegubowej, natomiast drugim końcem B podparta na podporze przesuwnej, poruszającej się na podłożu o kącie pochylenia cc * 30°. W punkcie C belki, odległym o y od jej prawego końca, działa siła P = 3000 N tworząca z osią belki kąt fi * 60°. Obliczyć reakcje podpór.

Rozwiązanie

Uwolnioną od więzów belkę pokazano na rys. I.40b, gdzie zamiast sił P, R_a i R₀ zaznaczono składowe tych sił (poziome i pionowe). Ze względu na znane kierunki działania siły P oraz reakcji R₀, ich składowe wynoszą odpowiednio:

^Px -	P	cos fi,	Py * P sin fi ;
^R8x -	^rb	sin cc.	^Rey * ^RB ^cos“-

Równania równowagi mają postać

^£pix - ^Rax - ^px - ^RBx ■ ^RAx - ^P cosP - ^RB ⁸ⁱⁿ“ * °'

^2piy " ^RAy " ^G ' ^py ^{ł R}sy * ^RAy " ^G “ ^p Bin/3 * ^rb ^cos“ ⁼

£m

^g4* Py-T¹ - V ¹

G j ♦ p| 1 sin fi +

- R_q • 1 cosoc _s O.

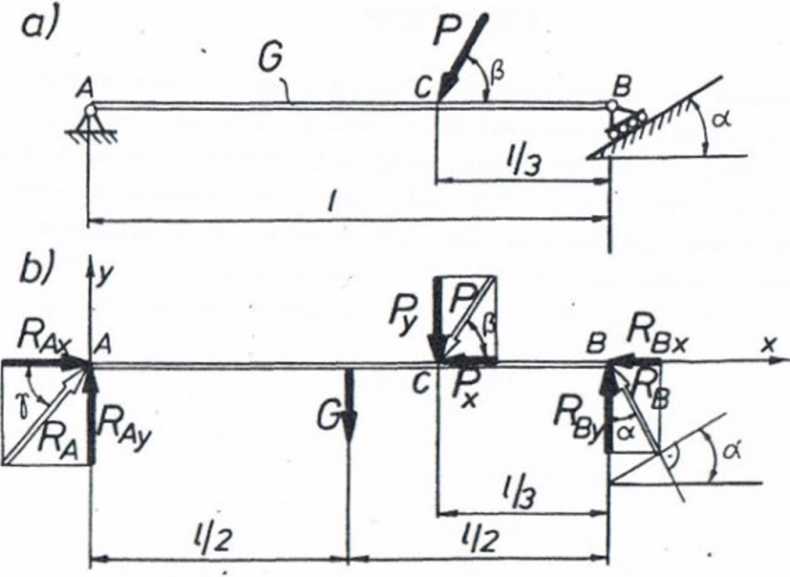
Rys. 1.40

W powyższym układzie trzech równań występuję trzy niewiadome: R_Ax. ^RAy oraz R₀, które łatwo można obliczyć rozwięzujęc kolejno równania: trzecie oraz pierwsze i drugie. Otrzymujemy

|g *|p sin/3 ^B    cosec-= ^24t*

R_Ax « P cos/3 + R₀ sina ■ 2731 N,

R_Ay ** G ♦ P sin/3 - R₀ cosa » 1266 N.

Prostota rozwięzania wynika z faktu, że w trzecim równaniu występuje tylko jedna niewiadoma R_Q, natomiast w równaniach pierwszym