270 (10)

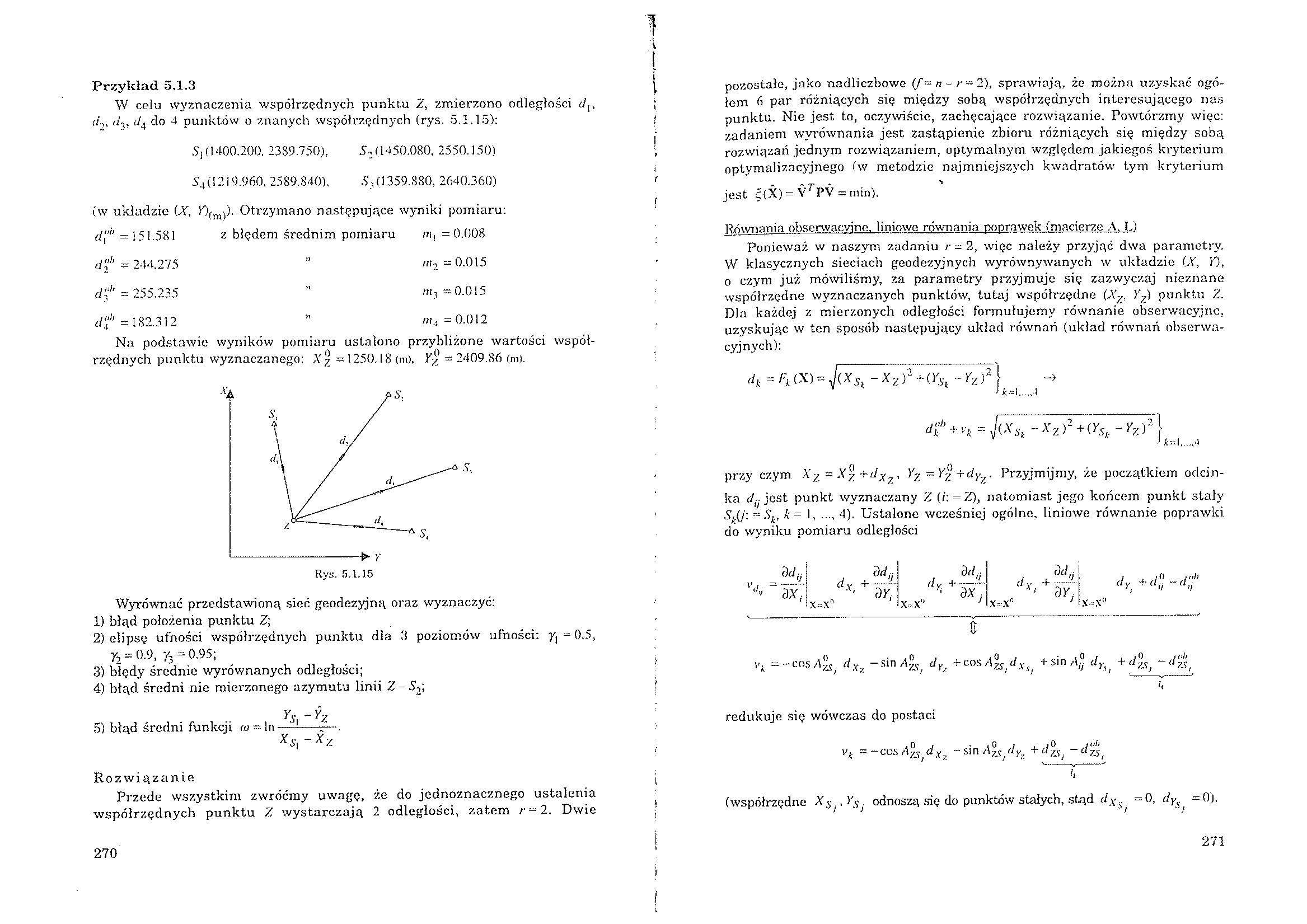
Przykład 5.1.3

W celu wyznaczenia współrzędnych punktu Z, zmierzono odległości d,, rt'-,. d-., f/₄ do 4 punktów o znanych współrzędnych (rys. 5.1.15):

,S*i (1400.200. 2389.750),    5, (1450.080. 2550.150)

S₄ (1219.960. 2589.840). S_} (1359.880, 2640.360)

(w układzie {X,    Otrzymano następujące wyniki pomiaru:

d\"‘ =151.581    z błędem średnim pomiaru tn, =0.008

df = 244.275    ”    nt ₂    =0.015

df = 255.235    ”    m₃    =0.015

df - 182.312    ”    />i..    = 0.012

Na podstawie wyników pomiaru ustalono przybliżone wartości współrzędnych punktu wyznaczanego: Xy =1250.18 (m), Yy =2409.86 (m).

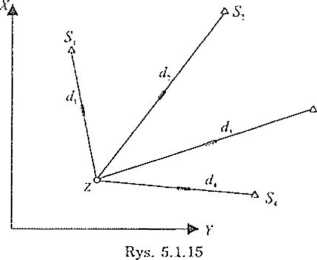
Wyrównać przedstawioną sieć geodezyjną oraz wyznaczyć:

1)    błąd położenia punktu Z;

2)    elipsę ufności współrzędnych punktu dla 3 poziomów ufności: y, - 0.5, y₂ = 0.9, y, - 0.95;

3)    błędy średnie wyrównanych odległości;

4)    błąd średni nie mierzonego azymutu linii X-S₂',

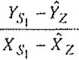
5) błąd średni funkcji io - In

Rozwiązanie

Przede wszystkim zwróćmy uwagę, że do jednoznacznego ustalenia współrzędnych punktu Z wystarczają 2 odległości, zatem r — 2. Dwie

pozostałe, jako nadliczbowe (f~n-r- 2), sprawiają, że można uzyskać ogółem 6 par różniących się między sobą współrzędnych interesującego nas punktu. Nie jest to, oczywiście, zachęcające rozwiązanie. Powtórzmy więc: zadaniem wyrównania jest zastąpienie zbioru różniących się między sobą rozwiązań jednym rozwiązaniem, optymalnym względem jakiegoś kryterium optymalizacyjnego (w metodzie najmniejszych kwadratów tym kryterium

jest ę{X) = V^rPV=min).

Równania obserwacyjne, liniowe równania poprawek (macierze A. L)

Ponieważ w naszym zadaniu r -2, więc należy przyjąć dwa parametry. W klasycznych sieciach geodezyjnych wyrównywanych w układzie (X, >0, o czym już mówiliśmy, za parametry przyjmuje się zazwyczaj nieznane współrzędne wyznaczanych punktów, tutaj współrzędne {X_y, Y_y) punktu Z. Dla każdej z mierzonych odległości formułujemy równanie obserwacyjne, uzyskując w ten sposób następujący układ równań (układ równań obserwa-

% _av'/

ód-	ód j
d + ± ^X' ÓYt	dy +—i
	^Yi ÓX.
X-X^n

cyjnych):
	kxSt-X7y--HYSl	~>z )M >k~\.....4
	df>	• vk - ^j(Xsk -xzy + (YSf. - >'z)" | f ^ ^
przy czym Xy =	x?.+‘iXz, yz = y|	-5- dYy ■ Przyjmijmy, że początkiem odcin

ka djj jest punkt wyznaczany Z (/: = Z), natomiast jego końcem punkt stały S_k(J: -S_k, k -- 1, ..., 4). Ustalone wcześniej ogólne, liniowe równanie poprawki do wyniku pomiaru odległości

v_k = - cos Ay_S d_Xy - sin A_ys d_Y/ + cos A_ys d_x{ + sin A® d_r^ + d_ys^

redukuje się wówczas do postaci

v_k ~-cos A_ysd_X7 - sin Ay_Sd_Y?    -d_y}_t

V.    V

(współrzędne X_S.,Y_S. odnoszą się do punktów stałych, stąd dx_s. ~^Y_s ⁼ A).

271