278 (9)

y~ 0.9

— dla wartości prawdopodobieństwa

odczytujemy F_v^_n(> - 9.00. więc

a = i«₀^2Aj ¹ Fy_₀_9 = 1W2- 0.012 T¹ -9.00 = 40.0 (mm) a = /«₀ ^2/o¹¹ F_y~()}) ~ 1.04\/2 ■ 0.0194^_1 • 9.00 -31.6 (mm)

-dla wartości prawdopodobieństwaj~y=0.95} odczytujemy /^;'_v._₀,₎₅ =19.00, więc

a - m₀ y 2;.f^! /y0.95 = 1.01/2 ■ 0.012 r¹ • 19.00 = 58.2 (mmi

6 = w₀ /2A₂'^! /y₀₉₅ = 1,04•Jl • 0.0194“' • 19.00 = 45.9 (mm)

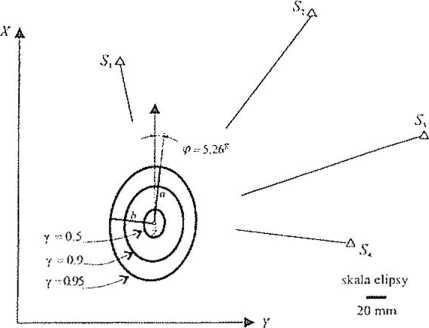
Rys. 5.1.16. Elipsy ufności. Sieć o mierzonych odległościach

3) Błędy średnie wyrównanych obserwacji - odległości

Kwadraty interesujących nas tutaj wielkości są diagonalnymi elementami macierzy kowariancji wyrównanych obserwacji x. Wyznaczając tę macierz, uzyskujemy

Ć₅ = >4 A(A⁷ PA)“’ ,\^T

57.19	37.19 10.69	-23.71'
37.19	64.12 63.03	40.86
10.69	63.03 80.74	74.59
23.71	40.86 74.59	89.14
).	m - = V 64.12 = a 2	8.0 (mm)
).	m~ =789.14 = a.\	9.4 (mm)

(mm)"

a na jej podstawie

ni % ~ J51A9 =7.6

«i

^mh

27S

Takie same wyniki uzyskamy korzystając ze wzoru na błąd średni funkcji

^ma> ~ ^m0    (A^rPA)~' F_ftł

przy ozy dla każdej, A'-t.ej odległości zapiszemy F^    Sprawdźmy, że

np. dla odległości : a^. =(-0/1297 -0.9030], i rzeczywiście

m - mo ya^.{A ‘^rPA)~^l a^_# =9.0 (mm)

4) Błąd średni azymutu linii Z-S,

Błąd średni nie mierzonego azymutu A^, po wyrównaniu, obliczymy korzystając z przywołanego w poprzednim punkcie wzoru na błąd średni funkcji. Ponieważ

^rSi " h

^AZSi - arctg-~-=-.......—

^As₂

więc (podobnie jak w przypadku liniowego równania poprawki do azymutu)

T«'    — J?

¹ (.0 ~~ ^K Ayję*,

^^azs2
()Xy		d?
^1 d^AZS2		A^zs-,
L „		4 J

= 10'

0.0024 - 0.0034

(mm)

Wyznaczając wartość interesującego nas błędu średniego, uzyskujemy "M_Bj =",„^_!2(^a'p^a)-V,₂ =0.00003«I2-p“=23“

^Y* -r_z

5) Błąd średni funkcji co -- ln Ustalając, że

F

dco

dXy

()(o dY~

(X_Sl-X_Zy

s-\

-0.00671

-0.°002j_(ln)-'

-(^ -y_zr

oraz korzystając ze wzoru na błąd średni funkcji, otrzymujemy m_(!1 = m₀ fil (A ^r P A) “^l F_f„ =0.0499 (bez miana)

279