2 (1686)

44

Ciągi liczbowe

będziemy zajmowali się wyłącznie ciągami liczbowymi i dlatego będziemy pisali krótko ciąg zamiast ciąg liczbowy.

© Przykład 1.1.2

Ciągi możemy określać:

A. wzorem:

a) a_n = 2ⁿ;

b) ó_n = —

1

Podstawowe określenia

C)

1.5

1

0.5

^c) c_n = y/nTT - Vn;

si nn

d) d_n — 1 + 2² -ł- 3^ -j- ... -f- nⁿ \

^e) — —t-

n n + 1

1 1

+

1

n + 2 ⁺ " ‘ ⁺ 2n’

[ 3ⁿ dla n nieparzystych, 0 fn ~ { _n3 ^la _n parzystych.

B.    rekurencyjnie (tzn. każdy wyraz ciągu wyraża się przez poprzednie):

a)    a\ = 7, a_n+i = a_n + 3 - ciąg arytmetyczny;

b)    bi — l,b_n+i = 2b_n - ciąg geometryczny;

c)    ci = 1,C2 = l,c_n+2 = c_n + c_n+ \ - ciąg Fibonacciego*;

d)    d\ — 2, d_n^.i — d\d2 • • • d_n.

C.    opisowo:

a)    a_n - n-ta cyfra po przecinku w rozwinięciu dziesiętnym liczby 7r;

b)    b_n - n-ta liczba pierwsza;

c)    c_n - przedostatnia cyfra rozwinięcia dziesiętnego liczby (n + 3)².

O Ćwiczenie 1.1.4

Znaleźć wzór określający a) (a_n) — (1,3,5,7,9,11 c) (c„) = (1,1, 2, 2,3,3,. e*) (e_n) = (1,2,2,3,3,3 g*) (g_n) = (1,1,2,3,5,8 i*) (i_n) =(1,0,2,0,3,0,

• Definicja 1.1.5 (ciągi 1. Ciąg (a_n) jest ogranie

O Ćwiczenie 1.1.3

Do podanych ciągów wskazać odpowiadające im wykresy: \    ⁵    ._{x L} 5n

Obrazowo: ciąg jest ogra prostą poziomą (rys. l.\ nieograniczonym z dołu.

2. Ciąg (a_n) jest ogranie

n + 2 ’ c) c_n = \/4;

n-f 2’

y/n.

Obrazowo: ciąg jest ogra: prostą poziomą (rys. 1.1 nieograniczonym z góry.

B)

6    8    10 n

^{2    4}    6    8    10 n

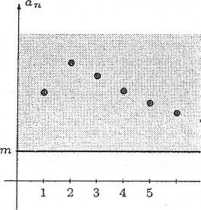
Rys. 1.1.2. Wykres ciągu z dołu.

* Leonardo Pisano Fibonacci (1170-1250), matematyk włoski.