2 (1930)

1 odpowiedzi I -s. 159

. ZBIORY, PRZEDZIAŁY I NIERÓWNOŚCI

c) A \ B,

a) An JB,

d) (AuJ5) \ C,

e) (BnC)\ A.

d)    A = (—oo;2), B = ( —oo;0)

e)    A = (-oo;3), B = (3;oo)

f)    A = (-oo;5), B- (5;oo)

Zadania powtórzeniowe

Zestaw A. Zadania powtórzeniowe 1 „ Wyznacz wszystkie elementy zbiorów A i B. Czy prawdziwa jest któraś z relacji A c B,

5cA?

a)    A - zbiór liczb naturalnych x spełniających warunek: x ^ \/26 B - zbiór liczb całkowitych x spełniających warunek: ~2yx^6

b)    A - zbiór liczb całkowitych x spełniających warunek: -27 <x³ <27 B - zbiór liczb naturalnych x spełniających warunek: x³ < 8

2.    Który z podanych zbiorów jest zbiorem dwuelementowym, a który jest zbiorem pustym?

A - zbiór liczb rzeczywistych, których kwadrat jest równy 8

B - zbiór liczb rzeczywistych, których sześcian jest równy 8 C - zbiór liczb wymiernych, których kwadrat jest równy 9 D - zbiór liczb całkowitych, których sześcian jest równy 9

3.    Wyznacz zbiory: Au B, AnB, A \ B i B \ A.

a) A = {3,4,5}, jB = {1,2,3}    b) A = {3,4,8,9}, B = {3,9}

4.    A jest zbiorem dzielników liczby 24, a B - zbiorem dzielników liczby 30. Wyznacz zbiory: AuB, AnB, A\ B i B\ A.

5.    A jest zbiorem spółgłosek w słowie matematyka, B - zbiorem spółgłosek w słowie trygonometria, a C - zbiorem spółgłosek w słowie planimetria. Wyznacz zbiór:

b) jBn C,

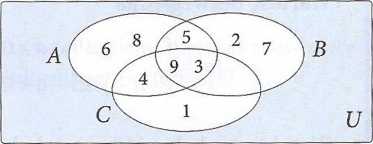
6.    Korzystając z diagramu obok, wyznacz zbiór:

a)    AuC,    d)    (Au5)\ C,

b)    BnC,    e)    Au(B\C),

c)    B \ A,    f)    C\(AnB).

7.    Wyznacz zbiory: AuB, AnB, A \ B i B \ A.

a)    A = <-l;3),B = (0;oo)

b)    A= (—oo;2), JB = (—3;2)

c)    A=(-oo;l),B = {4;oo)

8. Wyznacz zbiory: AuB, AuBuC, AnB, AnBnC.

a) A = {-3; 3), B = (l; oo), C = (-oo;2)    b) A = (4; oo), B = (1; 5), C = (2; 3).

14