324 2

324

•3. Równania różniczkowe

^c,ow Progr*. Postaci autono-

Dla układów równań różniczkowych zwyczajnych opracowano wiele pakietów mów; zob. np. Gcar [108]. Zakłada się w nich często, że układ jest dany w postaci micznej

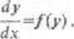
tzn. że/nie zależy jawnie od x. Układ nieautonomiczny łatwo przekształcić w autoń^. miczny, dołączając trywialne równanie

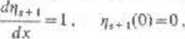
mające rozwiązanie rj_l+1 (x) = x.

8.1.2. Przenoszenie się błędów

Rozwiązanie zagadnienia początkowego (8.1.2) można uważać za funkcję y{x, c). gdzie c jest wektorem warunków początkowych. I w tym przypadku można przedstawić graficznie rodzinę rozwiązań_T tym razem w przestrzeni (x, y), gdzie poszczególne rozwiąza-nia odpowiadają różnym wartościom początkowym >»(«)-c. Dla s= 1 rodzina rozwiązań może wyglądać np. tak, jak na rys. 8.1.2 lub 8.1.3. Zależność rozwiązania y(x, c) od c jest często bardzo istotna dla problemu naukowego lub technicznego, z którego równanie pochodzi, a także dla rozwiązywania numerycznego tego równania.

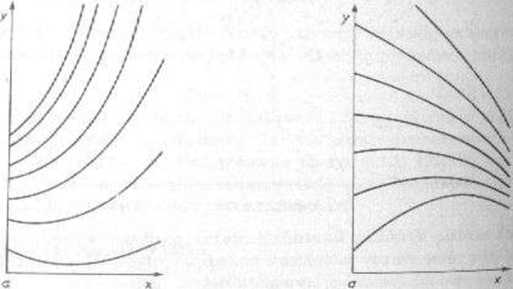
Rys. 8.1.2

Rys. 8 t-5

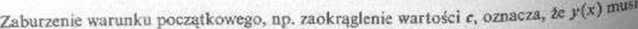
ymip.nić slena inny element rodziny rozwiązań, war

Przez metodę jeanoKrozową rozumiemy ta&ą meioaę, w Której odjiczając y_n* i