349 2

349

8.4. Szkic metod rozwiązywania zagadnień brzegowych i własnych

>todzie strzałów rozwiązuje się to równanie np. metodą siecznych (zob. § 6.4). Wybiera . __óbną wartość y₀ i oblicza się (w przybliżeniu) g(y₀), rozwiązując zagadnienie począ-we (8.4.3) jedną z metod opisanych w § 8.2 lub § 8.3. Wybiera się następnie inną wartość ¹ oblicza się w ten sam sposób g{y_x) (rys. 8.4.1), a wtedy z (6.4.1) wynika kolejno, że

7i ~7o

9(?i)-9(Vo)'

73=72-^(72)“^)

72-7j

^(72)“^(7i)

Można pokazać, że jeśli równanie (8.4.1) jest liniowe, to nawet wtedy, gdy jego współczynniki zależą od x> równanie (8.4.4) też jest liniowe (względem y). W takim przypadku już y_a jest rozwiązaniem równania (8.4.4) (oczywiście, jeśli pominie się błędy dyskretyzacji i błędy zaokrągleń popełniane przy obliczaniu 0(y_o) i g(y_t)).

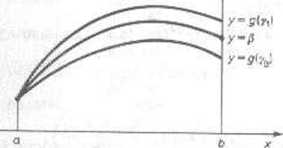
Rys. 8.4.1

Zdarza się czasem, te zagadnienie początkowe (8.4.3) jest źle uwarunkowane — nawet wtedy, gdy zagadnienie brzegowe (8.4.1), (8.4.2) jest dobrze uwarunkowane. W takich przypadkach korzystniejsza jest metoda z § 8.4.3. Tnną możliwością jest wielocelowa metoda strzałów; zob. Keller [112].

W wielocelawćj metodzie strzałów przedział [a, b] dzieli się na p podprzedziałów [x,_ _l, *4 ^xo-a, x_p=b. Wprowadza się nową zmienną niezależną t taką, te te [0, 1]. Rozwiązanie y(x) zastępuje się wektorem 2p-wy mi arowym

^(0=l>i(r), y₂(r),.... y^t), y[(t). y_a(f),..., j>;(i)]

te ył(f)=>(x_J_,-ff(x,-x_ł_₁)), tzn. y, jest fragmentem rozwiązania w [x,__Ł, X|}. ^ wnanie różniczkowe z (8.4.3) zastępuje się układem równań rzędu pierwszego y = *v(f, y), a oprócz dwóch warunków z (8.4.3) dołącza się do tego układu warunki ciągłości:

yi*i(0)    >•;(!)

*1+1 ““^xt —

to szczególny przypadek zadania określonego równaniami (8.4.11) i (8.4.12) z § 8.4.3). Ig^tySńdG tego układu metodę strzałów, otrzymuje się układ 2p równań względem wek-