378 (6)

8.2. Wybrane funkcje tłumienia

Funkcja Hubera

Funkcja tłumienia Hubera (np. 1981) jest funkcja o postaci (dla v~v/o oraz A'v=(-k:k))

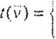
1    dla Av

0    dla v es Av

skąd wynika następująca funkcja wagowa

p ~ t(v)p ~ {

(0

dla v € Ar dla v £ Aż

(8.5)

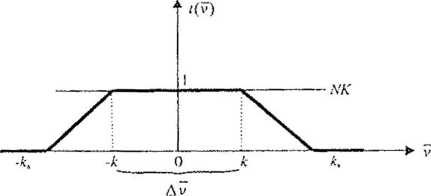
Jest to więc funkcja „radykalna”, przyporządkowująca zerowe wartości wag wszystkim obserwacjom, których poprawki nie należą do przedziału dla nich dopuszczalnego (taką funkcję stosowaliśmy we wcześniejszym omówieniu). Przebieg funkcji tłumienia Hubera, w porównaniu z funkcją tłumienia klasycznej metody NK (w której dla każdego v :/{v) - 1), przedstawiamy na rys. 8.3.

/(v)

■ NK

A v

Rys. Funkcja tłumienia Hubera

Funkcja Hampela

Ze względu na wskazywany wcześniej margines błędu decyzyjnego, a także niezerowe prawdopodobieństwa w odciętych „ogonach” rozkładów prawdopodobieństw, często przyjmuje się (o czym już mówiliśmy) mniej radykalne funkcje tłumienia (w porównaniu z funkcją Hubera). Do grupy takich funkcji należy funkcja Hampela (np. Hampku 19S6). Wprowadza się tutaj dwa dodatkowe przedziały pośrednie (na lewo i prawo od przedziału dopuszczalnego Aż), w których funkcja tłumienia r(ż) w liniowy sposób zmniejsza swe wartości. Funkcja tłumienia Hampela i wynikająca z niej funkcja wagowa mają następujące postaci:

1    dla ve (~k]k)

/(?) = ■	jvj“	h	dla	[vje (k\kh)	(8.6)
	I-	^ki>
	0		dla	M > ^kh
		p	dla	v 6 (~k; k)
p~t(v)p = -		f]v\-kh 1 ! ---...........- 1p	dla	jvj s (k\ k/})	(8.7)
		!v ^k - kh j
		0	dla	M > ^kb

gdzie k_h jest liczbą ustalającą granice dodatkowych przedziałów. Na ogół

przyjmuje się k_h~ 4.....6. Przebieg funkcji tłumienia Hampela przedstawia

rys. 8.4.

Rys. 8.4. Funkcja tłumienia Hampela

Funkcja duńska

Ogólne własności duńskiej funkcji tłumienia są podobne do własności funkcji Hampela. Jednak tutaj, poza przedziałem dopuszczalnym Av, funkcja tłumienia maleje ekspotencjalnie. Ponieważ oś v jest poziomą asymptotą tej funkcji, w omawianym przypadku nie ma potrzeby (w odróżnieniu od funkcji Hampela) wyróżniania przedziałów przejściowych i ich granic. Funkcja tłumienia i funkcja wagowa mają następujące postaci:

1	dla ve(~k\k)
[cxp{-/(jv[-*)M	dla Svi > k i 1
f p	dla ve (~k\k)
p = t(v)p-\ ,
[cxpH(|v[-A)^A } p	dla yi > k

379