37,38

zmiennej losowej U

F„(t) =

0

1    1    t

—+—arcsin—

2    7i U

dlat < -U

rnax

dla-U^

imx

l

dla t > U

max

i odpowiadającą jej gęstość

1

Urna* <t<U_max

dla

^fW=WuL-t²

q    dla pozost. t

Szukane prawdopodobieństwo otrzymamy pisząc

P(ju| > 0,5 •    ) = 1 - p(|U

max

<0,5-U_max)=l-F_u(0,5.U_niax)₊F_u(-0,5-U_irax) = ^

Podsumowaniem prowadzonych rozważań może być

Twierdzenie. Jeżeli X jest zmienną losową typu ciągłego o gęstości f skoncentrowanej na<a,b> (skończonym lub nie), funkcja h jest różniczkowalna, ściśle monotoniczna i odwzorowuje <a,b> na <c,d> to zmienna losowa Y=h(X) jest typu ciągłego o gęstości:

/(r'(;y))-|(/r¹(}’))j dla c<y<d 0    dla pozost. y

(27) g(y) =

Dowód. Rozważmy dwa przypadki:

funkcja h jest rosnąca. Wtedy z definicji dystrybuanty Y mamy

0

dla y <c

F_r (y) = P(Y < y) = P{h(X) <y) (h \y))

1

dla y > d

funkcja h jest malejąca. Wtedy mamy dla y e(c,d) F_Y(y) = l-F_x(h ^!(>0) • Różniczkowanie stronami w 1 i 2 daje tezę.

Charakterystyki liczbowe zmiennych losowych

Pojawienie się zmiennej losowej z jednej strony "zmatematyzowało" przestrzeń probabilistyczną (Q, A ,P). z drugiej jednak strony wykreowało pytanie o kształt

wykresu tej zmiennej losowej. Wprawdzie dystrybuanta daje pełny probabilistyczny opis zmiennej losowej, lecz jest to droga nadmiernej szczegółowości. W praktycznych zastosowaniach wykorzystuje się zaledwie kilka wielkości opisujących własności zmiennej losowej. Wielkości te nazywamy charakterystykami liczbowymi zmiennej losowej.

Def. Wartością oczekiwaną (przeciętną, średnią) funkcji zmiennej losowej Y=h(X) nazywamy liczbę:

^h(x_k) • p_k dla zmiennej losowej X typu dyskretnego

X_keW

o zbiorze punktów skokowych W = {x_px₂,...} i skokach p_k = P(X = x_k)

(28)    E(h(X)) =

+oo

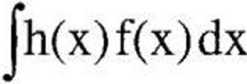
dla zmiennej losowej X typu ciągłego o gestosci f

—oo k

-t-oo

o ile zachodzi ^|h(x_k)|-p_k <°odla zmiennej losowej dyskretnej lub jjh(x)|f(x)dx <<*>

x_ke W    „oo

dla zmiennej losowej typu ciągłego. W szczególnym przypadku przyjmując h(x) = x

otrzymamy wzór na wartość oczekiwaną EX zmiennej losowej X. Wielkość EX możemy interpretować jako współrzędną środka ciężkości masy prawdopodobieństwa na IR¹.

Przykład 15. Niech zmienna losowa X ma skończony zbiór wartości punktów skokowych W={x-i, x₂₎ ... , x_n}. Niech każdą z tych wartości przyjmuje z jednakowym prawdopodobieństwem. Obliczyć EX.

38