img007u1

STATYSTYKA MATEMATYCZNA
ROZKŁAD BERNOULLl’EGO
Rozkład dwumianowy, dotyczący zmiennej losowej dyskretnej, jest oparty na doświadczeniach typu Bemou!li'ego, których schemat jest następujący:
wykonuje się serię n niezależnych doświadczeń w takich samych warunkach; w wyniku pojedynczego doświadczenia może zrealizować się pewne zdarzenie A z
prawdopodobieństwem P( A ) = p lub zdarzenie przeciwne Az prawdopodobieństwem P(A)
= i - p = q
Prawdopodobieństwo, że wśród przeprowadzonych n doświadczeń zrealizuje się k razy zdarzenie A jest określone wzorem:
'M -
P(X = k) = Qpk(l-Prk.
Dystrybuanta rozkładu dwumianowego przyjmuje postać:
Podstawowe parametry rozkładu:
pt(ł-p)"-k

Wartość oczekiwana Wariancja
Współczynnik asymetrii
F(X) = X
OSk<x
E(X) = np ;
D2(X) = np(l-p);
I - 2p
7| VnP(l-P> ’
Współczynnik spłaszczenia y, =---— .
np(l-p)
Kończąc charakterystykę rozkładu dwumianowego podkreślmy, że jego zastosowania praktyczne odnoszą się do obserwacji statystycznych prowadzonych na zmiennych dyskretnych dla małych liczebnie prób losowych (zwłaszcza w tzw statystycznej kontroli jakości produkcji).
ZADANIE 1 ótÓ fi. k\ 0.,.Vi
Wiadomo, że 1% skrzynek winogron psuje się w czasie transportu. Z transportu w sposób losowy wybrano 3 skrzynki. Niech X oznacza liczbę skrzynek z zepsutymi winogronami spośród trzech wybranych. Znaleźć rozkład prawdopodobieństwa zmiennej losowej X. Podać wartości prawdopodobieństw dla X=0, 1, 2 i 3. Obliczyć podstawowe parametry statystyczne tego rozkładu.
Wytwórnię wyposażono w 20 identycznych maszyn. Na podstawie doświadczeń stwierdzono, że prawdopodobieństwo wystąpienia awarii maszyny tego typu w ciągu jednego dnia wynosi około p = 0.05. Należy obliczyć, jakie jest prawdopodobieństwo, że

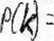
Urządzenie składa się z pięciu niezależnie pracujących elementów, Prawdopodobieństwo awarii dla każdego elementu jest równe 0.1. Wyznaczyć rozkład prawdopodobieństw liczby nie działających elementów.
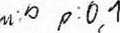
ZADANIE 4
W rodzinie jest troje dzieci. Obliczyć prawdopodobieństwo tego, że
1. W rodzinie jest nie mniej niż jeden chłopiec;
2. W rodzinie jest nie więcej niż dwóch chłopców;
3. W rodzinie są dwie dziewczynki.
Prawdopodobieństwo urodzenia dziewczynki jest równe prawdopodobieństwu urodzenia chłopca i wynosi : p = q = 0.5.
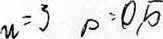

Wyszukiwarka
Podobne podstrony:
48572 img007u1 STATYSTYKA MATEMATYCZNA ROZKŁAD BERNOULLl’EGO Rozkład dwumianowy, dotyczący zmiennej
img007u1 STATYSTYKA MATEMATYCZNA ROZKŁAD BERNOULLl’EGO Rozkład dwumianowy, dotyczący zmiennej losowe
statystyka matematyczna cw3a STATYSTEMATYCZNA ROZKŁAD BERNOULLI EGO Rozkład dwumianowy, dotyczący zm
77114 statystyka matematyczna cw3a STATYSTEMATYCZNA ROZKŁAD BERNOULLI EGO Rozkład dwumianowy, dotycz
Strona 1 (14) STATYSTYKA MATEMATYCZNAROZKŁAD BERNOULLI EGO Rozkład dwumianowy, dotyczący zmiennej lo
Strona 1 (14) STATYSTYKA MATEMATYCZNAROZKŁAD BERNOULLI EGO Rozkład dwumianowy, dotyczący zmiennej lo
79138 stat Page1 resize Statystyka matematyczna 31 Definicja 3.19. Odchyleniem st
B Statystyka Matematyczna. Kolokwium zaliczeniowe 30 05 2016, B . 1. Zmienna losowa X ma rozkład geo
6 (2032) Biblioteczka Opracowań Matematycznych Ostatecznie więc rozkład prawdopodobieństwa dla zmien
6 Zbiór zadań z rachunku prawdopodobieństwa i statystyki matematycznej1.3. Schemat Bernoulliego 26.
rpism2 - RACHUNEK PRA WDOPODOBIEŃSTWA -ĆWICZENIA 2.ROZKŁAD PRAWDOPODOBIEŃSTWA I FUNKCJE ZMIENNEJ LOS
DSCN5043 Rozkład prawdopodobieństwa i dystrybuanta zmiennej losowej ciągłejDystrybuanta Fx(x) i -fun
68948 stat PageE resize Statystyka matematyczna 45 liczbę obserwacji, dla których
Rozkłady warunkowe WYKŁAD 3 Rozkłady warunkowe WYKŁAD 3 zmiennej losowej definiujemy
Rozkład prawdopodobieństwa danej zmiennej losowej -> funkcja przyporządkowująca wartościom zmienn
więcej podobnych podstron