37 (526)

Biblioteczka Opracowań Matematycznych

Współczynnik korelacji pomiędzy zmiennymi wyraża się wzorem (1.43): (!-⁴³)    _frr) (MUJ) F\UV)-EUEV

Obliczamy pomocniczo:

EU = E(aX + bY) = a£Y +bEY = am + to? = (a +

Z)²(/ = D²(aX +hY) = a² D² X +b²D²Y = a²cr²+b²(j² = (a² +/r)cr² U « yv((a + b)m\ ja² +b²<r)

£F = £(0^ -bY)- aEX -bEY = am-bm = (a-b)m D²V =    -£}) = a²Z)²X + b²D²Y = a²cr²+b²a²

V « At{[a-b)m:^j(a¹ + A²)tt)

£'(f/(^/)=    +    -*K)]=    -i’r^:]= £(a^;A-²)-£(6’r^:)=a²(«²A'+ (£A')^:)-

- A²(a>²K + (AT )^!)= a²(<r² + ot²)-A²(<x² + ot²)= (a² - A²)(<t² + m²)

Cov(U,V)= F.(U,V)~ EU -EV = (a^: - A^:X<r² + m²)- (a² - A^:)n² = (a²-Z>²)fcr²

Współczynnik korelacji zmiennych U i V jest zatem równy:

C°y{U,v)____    (a²-6²)j²    a²-A²

Jd²uJeŻv -Ja² + b²cr^a² +b²a a²+b²

/M=

98/ Gęstość dwuwymiarowej zmiennej losowej (X, Y) wyraża się wzorem: x+y dla jce<0,l>

0 poza

Obliczyć współczynnik korelacji tych zmiennych losowych.

Rozwiązanie:

Wyznaczamy gęstości brzegowe zmiennych X i Y:

f(*+>)£' =	y^2 ^V + 4-
0	2

1

= ,v + —

2 *

fy = {/(*, y)dx = J(.t+y)dx = y+-

-<x

I ( I

^£C⁰')=J| \{x+y)xydy dx=\ j(x²y + xy²}fy dx = J

^²

+ —

o v o

o V o

/

dx = -3

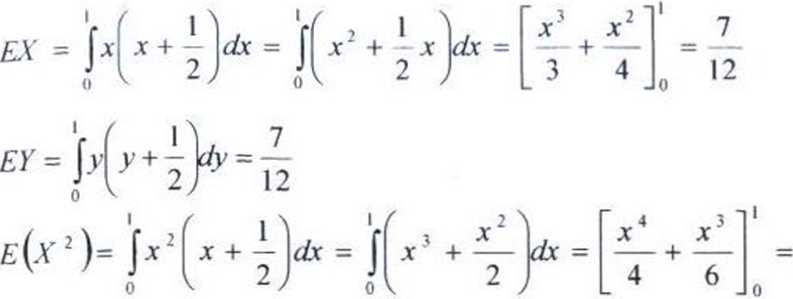
5

12

d²x = f\x²)-(exY =    —

12 144    144

D²K = £(r²)-(£K)² =

144

Podstawiając wszystkie otrzymane wielkości do wzoru (1.43) otrzymujemy:

1 _ 49

Cov(X,Y) _ ₃ 144 1_

11

P =

yj D²X yj D²Y

99/ Dwuwymiarowa zmienna losowa (X, Y) ma rozkład podany w tabeli 57. Tabela 57

II

144

X Y	1	2	3
4	0.2	0.1	0.5
5	0,1	0	0.1

Wyznaczyć współczynnik korelacji zmiennych X i Y. Wyznaczyć równania prostych regresji drugiego rodzaju.

Rozwiązanie:

W celu wyznaczenia współczynnika korelacji wyznaczamy rozkłady brzegowe zmiennych X i Y. Rozkłady te przedstawione są w tabelach 58 i 59.

Tabela 58.

Xi	1	2	3
p>	0,3	0,1	0.6

Tabela 59.

Xi	4	5
Pi	0,8	0,2

Wyznaczamy wartości przeciętne oraz wariancje dla zmiennych X i Y.

EX=f_ix,p_l = 2.3;    E(x²)=f.x?p, =6,1; D²X = e(x²)-(EX)² = 0.81

»=l

1=1

-73-