20 (4)

Biblioteczka Opracowań Matematycznych

Do obliczenia całek 118/ i 119/ zastosowano metodę współczynników nieoznaczonych.

120/ f(2x-5}j2+3x-x²dx = fi^-~-⁵fc ^{+ 3}-^r~^jr')_tfr = f-2.v^ł + ll.T--llT-10_d|f - ^{3    3}    V2+3x-x²    3    ■j2+3x~xⁱ

Dla wyznaczenia całki 120/ należy w dalszej kolejności zastosować metodę współczynników nieoznaczonych.

- = t

-di

f dx		1	_f t^2 _	f ^dt — f
xvl0x-	•> x~	— t	^JI 110 1	Il0t-l ^3
			n / t^2	1 r
>/-l = z^2		r

10 dt = 2zdz

dt = —zdz 5

= -- [dz = -±z+C = ~JWr-l+C = --J— -1 5^J 5    5    5 V x

121/ 1

C idt    j- dt

122/

J₇

(x + \)yjx² +2x+2 = - ln / + yjt² +1

+ C = - In

1

x+l 1

I

123/ J-

yl 10x-x²

	5x
dt		dt
l+r	^JVr +1
t^2
X + 1		+ C

+ 1

+ C = In -t³dt

x +1 Vlx + 1 I . dt

= i dx = -^ = \-t    r ^J

t

= -]-t-Jt² + 1 +-ln|/ + V/^J + l| + C =    + — In

2    2 1    I    2x‘    2

'4\7:

= - = / x =

/²<*

+i

+c

Dla wyznaczenia całek 121/, 122/, 123/ zastosowano poniższe podstawienie:

Dla całek*-_dx_

(x-kY yjax² +bx+c

należy podstawić (1.3 7)    ¹

x-k

=/

6. Całki funkcji trygonometrycznych

Jedną z ważniejszych metod całkowania funkcji trygonometrycznych jest zastosowanie jednego z podstawień tzw. uniwersalnego. Wzory

(1.38)    oraz (1.39) dotyczą właśnie tych dwóch podstawień. Podstawienia te pozwalają sprowadzić całkę zawierającą funkcje trygonometryczne do całki funkcji wymiernej.

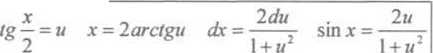
COS X = -

1 — u

1+u²

tgx =

2 u l-w²

(1.38)

(1.39)

124/

igx = u x = arctgu dx =

cos ‘ .r =

I

1+M²

2du

du

1 + m²

■ 2 » sin x =

1 + m²

dx

= f-»+«- .₌ f-

3simr+4cosx 2m , 1-m²

3--^ +4-r

I+M² 1+M²

du

2m‘+3m+2

-f

du

du

>(m-2)0 + 1)

1    A

hu-2x1+0"

_ _ B u(A + B)+A-2B

(m-2X2m + 1)"m-2 ⁺ 2m + 1^_ (m-2X2m + 1)

-2(m-2)^m+^

= /

2A+B=0 A-2B = -1

A=-¹-

5

S=²

5

. Ir du 2 c du i,.

/=— f-+- f-=—ldu-2-

5^jm-2 5^j2m+1    5 ¹ ^

1,

⁼ 5 I”

2m + 1	5	2«| + l
m-2		x ,
		^,gr^2

+ C

2M+l=t 2

-39-