392 (14)

- 393 -

392 -

3tosując twierdzenie de 1'Hospitala do wyprowadzonej w poprzednim

tu zależności i_p(t), dla cu_Q = 0, otrzymujemy    ^ ^z^P®d-

u (0)

iplt) = -i_p(0)(»t - l)e"‘*^t - -Łj■— t

t

jęli. ^R>

to

8₁ j “ ~ &¹- ~

Zatem, gdy R =<

ieat aperiodyczny

2.fk, przebieg czasowy składowej przej ściowe-j    , .

\y krytyczny i po podstawieniu zależności na i (o) i "“'TT

P ^{1 u}p'0)

ⁱp^tt) “ W “ ^l)e_<Xt ’ ³ⁱⁿ^~ 9) - |z7cugl * e"^Cttcos(y-_?). 3tąd prąd i(t)

l^E !    ie i

i (t) ³    3in(ajt + y - <j>) +    ■ (tjct - 1 Je^^sini y -(p) -

! I i —att    /    \

" ~[T\ uySL ^t 8 C°^BW~ f)»

Po podstawieniu danych

i(t) =. (13,6 aindOOOt + 0,72) +

+ S,97(5000t - l)e"^5000t - 2556Ht _e^_5000t) mA.

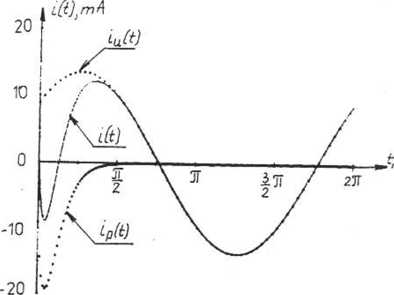
Przebieg i(t) przedstawia rys. 4.16.2.

mi

Rys. 4.16.2

Łjydwność R=-2^ jest spełniona

<* “ 2C

dla R = 480 9. i dla tej wartości:

^R = 6 . 10³ i,

Z³ ^ ~ TC ^a 3317

rad

I _tJB przypadku korzystając z uprzednio wyprowadzonych wzorów należy podstawić % = 3/3, a ponieważ:

sinj/3t =■ jsh/3. cos j/9t = ch^S,

to otrzymuje się

u (0)

ip(t) => -i_p(0)    sh^t - chyBt) -    — e sh^fjt.

Zatem, edy R > 2 jŁ nrzabiee czasowy składowej przejściowej prądu Lea.t aperiodyczny i po podstawieniu zależności na i_p(0) i u_p(0)

ip(t) =* -Jyp siniy- Cp)a~^AX{^ sh/Jt - ch/3t) - |Z| Lc/SL"

t,n?s

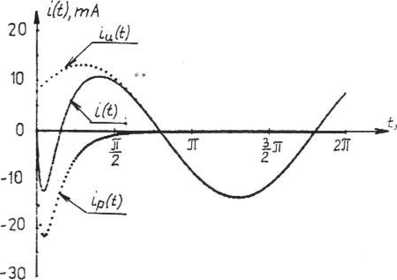
Rys. 4.16.3