410 (4)

Uogólniona odwrotność    o postaci (9.8), zastosowana do rozwiąza

nia sprzecznego układu równań Ad_x + L = 0, gdzie macierz współczynników A jest niepełnego rzędu, pozwala na spełnienie kryteriów (9.3). Oznacza to,

że odwrotność A(podobnie jak i inne warianty g-odwrotności) wynika

z rozwiązania pewnego problemu optymalizacyjnego. Problem ten, który w interesujących nas tutaj zagadnieniach nazwiemy zadaniem wyrównania swobodnego, można przedstawić w następującej postaci (np. Wolf 1972. 1979, Światek, Wiśniewski 1983):

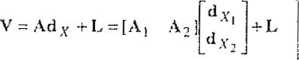
C_xoh -trjQ_x„_h -<7qP ¹

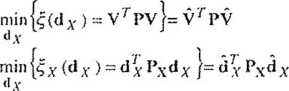
(9.9)

Wektor takich przybliżonych parametrów X^w, że X = X° + <i będziemy w celu zachowania ogólności przedstawianych dalej rozwiązań traktowali

jako zmienną losową o macierzy kowariancji C^o ⁼ <³‘ox Q_xo (w niektórych sytuacjach macierz wag P_x lub jej niektóre bloki niekoniecznie muszą być związane z modelem statystycznym, i w tym węższym sensie także odgrywać rolę regulującą procesem optymalizacji z zastosowaniem

ki*yterium d^TxJ>_xd_x - min).

Rezultatem poszukiwania minimum funkcji celu ę(dy) = V⁷PV względem dy jest, jak wiadomo, układ równań normalnych

A ⁷ P Ad_x +A⁷'PL =0

Stosując przyjętą już wcześniej strukturę macierzy

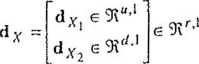
A -[ A, e 9i"’^H A₂e9i"‘^t/)eW^>‘^r,

(/• -- u + d), układ ten można rozpisać do postaci

A^y PA d y + A^rPL = O «=>

r a f i		d y, "		[Af^1
• ^ i \^TA 2	P[Aj,a2i	^A t *x2	X	aJ_

PL = O <=»

[a[pa, | A 2 P A |

aJ'pa2	~*xt]	Af PL
A 2 PA 2	- + <**,]	l E

lub, po wymnożeniu, przedstawić w postaci układu dwu równań macierzowych

(9.10)

A fPA |d y, + Al PA₂d Yi ⁺ A i PL ~    (« równań)* |

A2 PA jd _V| + A2PA ₂d y, + A₂ PL = 0 <— (d równań)** j

Równania drugiego (**) z tych ulcładów (w liczbie d) są kombinacją równań tworzących układ (*). Właśnie dlatego rząd f/f(A^rPA) =h] < r i macierz A^/PAe3\^r,r jest osobliwa. Wynika stąd, że jeśli wektor niewiadomych

d _Y -\&L dL )^r spełnia pierwszy układ (*), to musi spełniać także i rów-

nania drugiego układu (**). Pozwala to na zastąpienie układu dwu równań macierzowych (9.10) tylko pierwszym z nich, tzn.

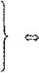
Af PA | d _x, + A f PA ₂d _x + A f PL = 0 AoPAjd y, +AjPA₂d_x, + A₂PL = 0

A f PA,d _x +A[PA₂dY, + Af PL = 0

To jedno wybrane równanie zapiszemy w następującej postaci;

Q)2

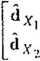
+ Af PL — 0

Af PA,d y, + Af PA₂d_V2 + Af PL = 0 <=> [Q,,

gdzie;

B=[AfPA,

Bd y + A =0

a[pA₂1 = (Q„ Q₁₂], A = A f PL

(9.11)

CQi j — Af PA [. Q, 2 - A f PA 2).

411