445 2

445

11.3. Zastosowania — Redukcja wariancji

Pytanie przeglądowe

Podać trzy metody redukcji wariancji przybliżeń konstruowanych metodą Monte ~-trlo i wyjaśnić* co ten termin znaczy. Jaki jest związek między redukcją wariancji i zmniej-k°^sztu obliczeń niezbędnych w danym zadaniu?

Zadania

I P|jjj o wysokości 2b i bardzo dużej szerokości jest ostrzeliwany z działa (założenie, & cel jest szeroki, sprawia, że zadanie jest jednowymiarowe). Odległość do środka celu _njr- jest znana: wiadomo tylko, że jest równa w przybliżeniu D. Różnica między rzcczy-wi.ęw odległością i przybliżeniem D jest z założenia zmienną losWą X o rozkładzie nor-nuthtytn z wartością oczekiwaną 0 i odchyleniem standardowym c,.

Do celu oddano salwę z trzech pocisków'. Szacuje się. że pociski przebyły' odpowiednio drogę D-a,D\D l-a. Różnica międzyrzeczy wistą przebytą odległością i tym przybliżeniem jest / założenia zmienną losową o wartości oczekiwanej 0 i odchyleniu standardowym o₂; składową błędu w tych trzech strzałach oznacza się Y.,, Y_a, Y_x. Zakładamy jeszcze, że ic trzy zmienne są stochastycznie niezależne między sobą i od X.

Chodzi o ustalenie, jak prawdopodobieństwo co najmniej jednego trafienia w danej salwie zależy od a i h.

Zastosować liczby losow^re o rozkładzie normalnym (zob. Dodatek) do „oddania" dziesięciu salw i wyznaczyć dla każdej z nich najmniejsze b, dla którego w tej salwie uzyskano ęo najmniej jedho trafienie. Wykazać, że jest ono rówaie

min|*-(y_i + te)| (i=-l,0, 1).

■ i

Oddać również dziesięć salw „przeciwnych".

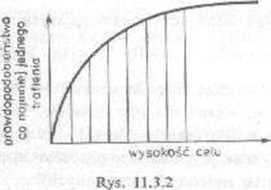
M^kjftólić dla <t, =3, a. = \ i dla dwóch, wartości a, równych I i 2 (przy tych samych - ⁷*bach losowych), zależność prawdopodobicńsrwa trafienia od wysokości celu (jak na *>^s 11.3.2).

Porównanie dwóch systemów obsługi (zob. rys. 11.3.3). Dziesięciu klientów przy-^{5 S}>'^{steciu w} momentach losowych, średnio co minutę. Wobec tego proces przy-klientów jest procesem Poissona z oczekiwanym odstępem między' kolejnymi równym 60 s. Stanowiska obsługi .41 i BI mają wspólną kolejkę. Klient wybiera