497 2

497

Rozdział 7

5. Propozycje: (a) j - ) f J‘. W pierwszej całce przyjmujemy x=f- i korzystamy

O O 16

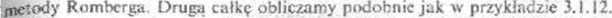
(b) Przyjmujemy sx = r i całkujemy metodą Romberga od / -O do t - 12. Resztę można jnąć. Postępując jak w przykładzie 3.2.6 można skrócić przedział całkowania.

(cj Obliczamy s_m— J metodą Romberga dla kilku n i stosujemy wielokrotne średnio-

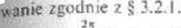
o

6. (a) J e'^kl dr=0 dla A=0 i 2k dla A^O. Stosujemy wzór trapezów do funkcji e^,kl

(A całkowite. A| ^/ik

h^ł+tⁱ0,rV²'^kA+...+irⁱ'^k+^e^,

1 tfCft

(A le'** ^l,m,— | )!(e^,kl>-• hin 4-1) =2k

h-n (k*G),

(A =0)

(zgodnie z wzorem na sumę szeregu geometrycznego). Dlatego wzór trapezów jest dokładny dla rozważanych funkcji wykładniczych, a więc i dla ich wszystkich kombinacji liniowych.

Uwaga. Wzór trapezów i wzór prostokątów są identyczne, gdy funkcję okresową całkuje się w pełnym okresie.

(b) Niech P będzie wielomianem trygonometrycznym takim, że \f[t)—P{t)|<£. Niech {_{ i Ip. będą całkami odpowiednio z //2jc i PJ2it, a T_f i T_P - przybliżeniami trapezowymi.

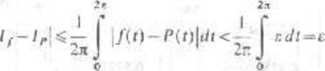
Wtedy

• podobnie jT_P- T_f\<t.. 7. nierówności trójkąta

2e .

|_//-T_/|<|/_/-/_P| ₊ |/,-T,| ₊ |T,-T_/|<. ₊ 0_ł«.

(Ten rodzaj analizy błędów ma szerokie zastosowanie. Zob. twierdzenie 4.5.2 i przy kład 4.5.3.)

,    (c) Korzystając ze wskazówki, otrzymuje się

2.03

^(5K— 2-*<2.5IO-«.

Stąd w zadaniu 3 jest J?_T<5 ■ 10 ⁸.

7. Odcięte v0.6, 0,- v'0.6 >ą zeranji wielomianu Legendre*a P₃(.r) = ^(x-‘    -*).

Współczynniki otrzymuje się łatwo (metodą współczynników nieoznaczonych) z żądania.

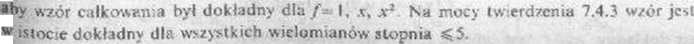
2vretodv n.umcrvc*ne