50 (341)

108

Funkcje zespolone zmiennej zespolonej

Im u;		Re ty= ^ i,
o		1 Re

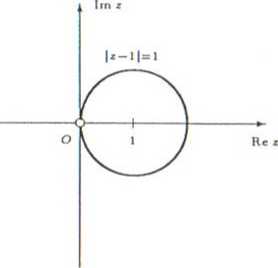
b) Niecił z jó — 1 oraz w yź 1. Wtedy

z + 1    tu — 1

Niech z = x + ty oraz tu = u -f tu. Wtedy wobec ostatniej równości mamy tu _ —u — tu _ (—u — tu)(u — 1 — tu) _ —tt² + u — u² + tu

tu — 1 u + iu—1

(u-l)² + u²

(u — l)² + u²

= x + iy

Stąd

—tt² + u — u²

(ti-l)² + u² °^raZ V (ti-l)²+U²'

Zatem

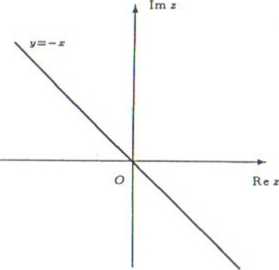
y = -x <=>

u² - u + u²

(ti-l)² + u² (u-l)²+u² u = u² — u + u² A (ti, u) y£ (1,0)

^ (^u4) ⁺(^v4)²⁼(t!) ^A(“^>,,)/(ll0)-

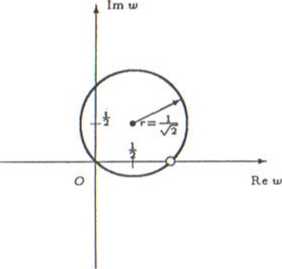
Obrazem prostej y = —z jest okrąg o środku    i promieniu -^= bez punktu (1,0).

> n, ,_vc. ,i ■> _r

’ ^{PrzyMad J b} ..

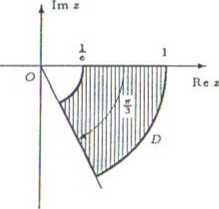
a) Znaleźć obraz pasa D = {z £ C : 0 ^ Re z ^ 1} przy odwzorowaniu w = e^z;

Trzeci tydzień - przykłady

109

b)

Odwzorować zbiór D =    C: - ^ |z| ^ l,

l ^e

funkcji ui = log z (logarytm główny).

^ argz

za pomocą

Rozwiązanie

a) Niech z = i + iy. Wtedy

c* = e*(cos y + i sin y).

Stąd |tu| = |e*| = e* oraz arg tu = arge* = y. Zatem

Re z

0 ^ Re z ^ 1 ą=> 1 ^ e sC e <==> 1 {C |w| e.

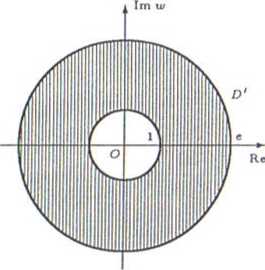
Ponieważ y jest dowolne, więc również arg tu jest dowolny. Tak więc obrazem pasa D jest pierścień

D' — {w ę. C: 1 ^ |ui| ^ e} .

Im z

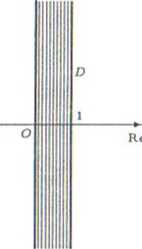
b) Mamy to = log z = ln |z| •+■ i arg z. Stąd Re tu = ln |z| oraz Im tu = arg z. Zatem

- ^ Izl ^ 1 ą=> ln — ^ Re tu ^ ln 1    — 1 ^ Re tu ^ 0

e    e

oraz

-- ^ arg z ^ 0 <=>• - j < Im tu ^ 0.

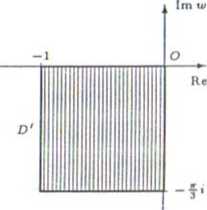
Obrazem zbioru D jest prostokąt

}■

D' = | tu g C: —1 Sj Re tu ^ 0,

^ Imtu $ 0