61 (160)

tii

s = R (1 - cos f) .    (2.19)

Zakładając, że do tyczenia punktów pośrednich łuku zastosujemy metodę biegunową oraz rzędnych od stycznej, przebieg wszystkich niezbędnych obliczeń będzie następujący:

a)    Obliczenie ;danych potrzebnych do wytyczenia punktów głównych łuku kołowego:

etyczna t = 50,00 tg 40°51'45^,ł = 50,00*0,865 082 = 43,25 m,

łuk PK = ł = 50,00 M-iff-^O" o 50,00*1,426 369 = 71,32 m,

■ 206 265"

cięciwa c = 2*50,00 sin 40°51'45" = 100,00*0,654 246 = 65,42 m,

strzałka s = 50,00 1 - 0,756 282 = 50,00*0,243 718 = 12,19 m.

Punkty główne P i K wyznaczymy w terenie przez odmierzenie|od punktu wierzchołkowego W odcinków t = 43,25 m wzdłuż obu | stycznych. Punkt środkowy łuku S wytyczymy przez odłożenie w połowie cięciwy długości strzałki s = 12,19 a (rys. 2.15.) .

b)    Obliczenie danych potrzebnych do tyczenia punktów pośrednich łuku metodą biegunową (rys, 2.16.) , dla n = 10 równych odcinków na łuku. Obliczenia dla połowy łuku zestawiono w tab. 2.6.

X

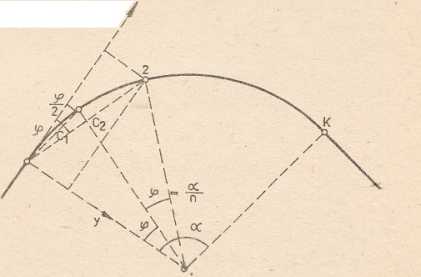
Rys. 2.16. Tyczenie punktów pośrednich metodą biegunową