61 (258)

4

Szeregi zespolone

Siódmy tydzień

Przykłady

Przykład 7.1

Zbadać zbieżność i zbieżność bezwzględną podanych szeregów:

3"    _v^(l + t)ⁿ

' n^32" ’ n = l	oo ■»£ n=0
di V ^2n + i-^d)^,V + l’ n = 1	oo •>E n= 1

OE

n i

n=i n2²

^{n=i n!} (^e+0

Rozwiązanie

a) Zbadamy najpierw zbieżność bezwzględną. Mamy

5>i-£

oo ^

Szereg £ —

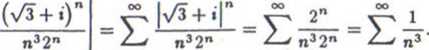
n= 1    n= 1    n=* 1

jest zbieżny, co oznacza, że badany szereg jest zbieżny bezwzględnie,

n= 1

więc także zbieżny.

b) Stosujemy kryterium Cauchy’ego. Mamy

Ponieważ

więc badany szereg jest rozbieżny, zatem nie jest również zbieżny bezwzględnie.

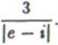
Siódmy tydzień - przykłady    131

c) W tym przypadku, jak w punkcie a), zbadamy najpierw zbieżność bezwzględną. Mamy

5>i-E

(i + 0ⁿ

n2 '

^u+.r ^ (v^/2)^,‘ ^ i “2-r s ~ 2^ z ⁼Z^ń

n= 1    712    nsl 712    na 1

Szereg — jest rozbieżny, co oznacza, że badany szereg nie jest zbieżny bezwzględnie. Z—/ n n= 1

Zbadamy, czy jest on zbieżny. W tym celu wykorzystamy kryterium Dirichleta. Przed-

1 ,    (1 + i)ⁿ ...

stawmy n-ty wyraz szeregu w postaci z„ = a„ -6,,, gdzie a_n = —, b„ = --r-, Wyrazy

" 2³

ciągu (a_n) = ^ —^ są rzeczywiste, dodatnie i maleją do 0. Zbadamy teraz ograniczoność

OO

ciągu sum częściowych szeregu ^^4_n. Jak łatwo zauważyć, jest to szereg geometryczny

o ilorazie o =    . Zatem

V2

i +»

V2

H#)1

1+2

V2

\/2 - 1 + «'

Ponieważ dla n g N punkt 1

i±*V

V2 )

ffl

należy do okręgu o środku O i promieniu 1, więc

<C 2. Stąd mamy

|l + ‘l

|S„| =

-(W)"

2y/2

\V2-1 +«|    " sj\ - 2v/2

Oznacza to, że ciąg sum częściowych szeregu    jest ograniczony. Zatem na mocy

n=l

kryterium Dirichleta badany szereg jest zbieżny.

d) Zbadamy najpierw zbieżność bezwzględną szeregu, wykorzystując kryterium porównawcze. Zauważmy, że dla każdego n 6 N prawdziwe są nierówności

I Z" =

in³ -f 1 I

Ponieważ szereg — jest zbieżny, więc z kryterium porównanwczego wynika, że także *^f n⁴

n= 1

Ei 2n + i I .

| -_n3 ₊ } | J^est zbieżny. Zatem badany szereg jest zbieżny bezwzględnie, a więc

także zbieżny.