88 89 (11)

- Przekształcenia liniowe

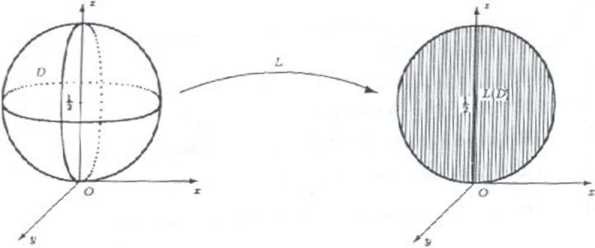
Zbiór L[D) jest zatem kołem o środku (0,0, -j i promieniu leżącym na płaszczyźnie zGz. Przedstawia to poruszy rysunek:

' 1 0 C ' 0 0 0 0 0 1

, więc rzeczywiście zachodzi w2Ór

Ponadto A —

|£(0)I = O=| .0 = P| |dety!|.

• Przykład 9.5

Rozwiązać ponownie Pr2ykad 9.2 stosując tym razem wzór na zmianę macierzy przekształcenia liniowego przy zmianie baz wychodząc od baz standardowych rozważanych przestrzeni liniowych.

Rozwiązanie

Macierze A i A' przekształcenia liniowego L : U—► V w bazach „starych" obu przestrzeni liniowych i w „nowych" bazadh tych przestrzeni związane są zależnością

A' = A P,

gdzie P oznacza macierz przejścia z bazy „starej" do „nowej" przestrzeni U, zaś Q jest macierzą przejścia z bazy „starej" do „nowej" przestrzeni V. We wszystkich przykładach bazami „starymi" będą bazy standardowe odpowiednich przestrzeni. Mamy zatern:

a)

A'

b)

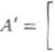
1

1

1 0 0' -1 1 0 0 -1 1

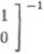
' 1 1 2 1 1 -3

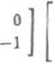
111'

2 1 1 2 1 2.

1 1

1 -1

10 0		' 2 0'		2 0'
1 1 0		3 1	=	5 1
.111.		-2 4.		.3 5.

-10 ol

0 0 -1 J

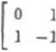
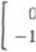
0

0

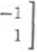
1 -1 0 1

2 3	-i	-10'	r-3 2		■ _J_ _3_ 10 10		3-2		-6 1 -5 2
4 1		^01J	L ^5 >J		2 1 5 5 -		5 1		IN

\i	-1	1 - 2		' 0	0	0 '		-2	0	—4 '
l	-1	1		1	-1	3	=	0	2	-2
2		2		2	2	2 .		1	-1	3 .
. 0	1	0 .

• Przykład 9.6

Napisać macierze podanych przekształceń liniowych L : U —► U w podanych bazach przestrzeni U. Zastosować wzór na zmianę macierzy przekształcenia przy zmianie bazy:

a)    L(i,y)= (3x-4y,2x + y), U = R², Si = (1,-1), u₂ = (3,2);

b)    /, jest symetrią względem płaszczyzny yOz, U = R³, 5i = (1,2,0), U2 =

(0, —1,1), u₃ = (0,2, -1);

c)    (Łf>)(z) = (c+l)p(3), 17= Ri[st], Pi = x + 4,p₂ = 2x-3.

Rozwiązanie

Niech P będzie macierzą przejścia z bazy „starej” przestrzeni U do bazy „nowej*. Wzór na macierz A' przekształcenia L w „nowej* bazie przyjmuje w tym przypadku postać A' = P~^lAP gdzie A jest macierzą przekształcenia i w „starej” bazie. Przyjmujemy bazy standardowe przestrzeni U jako bazy „stare” i otrzymujemy wzory a)

	-i						■ u	22 *
13'		3-4]	f 1 3'	_ 1	2 —3 1	r^711 _	5	5
-1 2		2 1 J	[-1 2	“ 5	.1 ^1 J	l^1 sJ ~	8	9
							- 5	5 -

b) Ponieważ L(x, y, z) = (-r, y, z), zatem

' 1 0 0	-i	o o •—1 1		o o
2-1 2		0 1 0		2-12
. 0 1 -1j		0 0 1.		i 7 o

cl)

112'	-i	'0 0 0'		4 6 5'
0 U 1		0 l 0		1 -1 3
-110.		.001.		. 2 2 2.

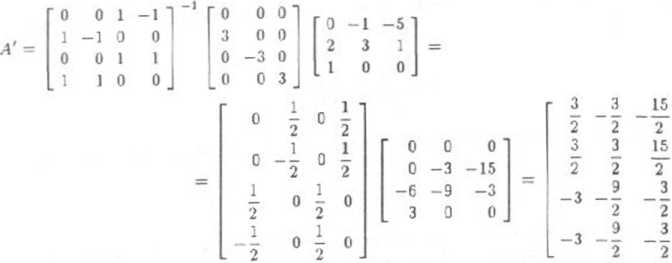
e) Z tego, ze i,(l) = 3z, L(r) = -3x², I (r²) = 3r^a wynika, że