bo3

mm

Łącznie na 25,0 pkt. uzyskano

.uzyskano

/

Pytanie 1......................................................................................................za 2,5 pkt. .......

Proszą wygenerować 4 liczby losowe o podanym niżej rozkładzie^ empirycznym pfckAAfeerocesie generowania proszą przyjąć, że pierwsze cztery liczby z generatora liczb - losowych o rozkładzie równomiernym na przedziale <0;1> są następujące: 0,49366353499;

0,73945614474; 0,85717559222; 0,76177534100. ^

'0,05    dla    z = 10    1-sza liczba:

0,35    dla    z = 12    2-ga liczba:

0,40    dla    z = 14    3-cia liczba:

0,20    dla    z = 16    4-ta liczba:

p{z) =

r-

or-u-

c,(r

-j

3

Pytanie 2....................................................................fżTffL.jHS..................za 1,5 pkt..............uzyskano_

Która z przedstawionych zależności jest matematycznym odwzorowaniem ll-szei formuły Little’a {proszę zaznaczyć obwódką

prawidłowe odpowiedzi) oraz objaśnić znaczenie użytych w tej zależhości zmiennych.

---

kWZo.

Ułta

j. w <    --

~ ''oczek.

♦ L

X*

oczek.

® ^Woczek. “—Roczek.

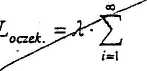
^oc:eJt.Sv ^ oczek. ~ ^ ^oczek.

Objaśnienia zmiennych:

Pytanie 3......................................................................................................za 2,0 pkt.............. uzyskano __

Proszą uzupełnić graf stanów jednofazowego systemu obsługowego M/M/n/0, jeżeli czas między zgłoszeniami ma rozkład wykładniczy o funkcji gęstości prawdopodobieństwa f(t) = A-e~^Xl. Do wykonywania obsług zgłoszonych obiektów przewidziano stanowisko obsługowe. Czas obsługi obiektów na stanowisku ma rozkład; wykładniczy o funkcji gęstości

prawdopodobieństwa postaci /(r) kb    74    /L

,_M._r

^    71'^

i.

ł

±

-

S0

Si

S2

Sk-1

Sk

Sk+1

Sn

t_

ł

'f"

_Jł_

+■

TT_

i.

^M. jks~4jjLk.

{k±.Vj^

a 2,5 pkt/......r......uzyskano_

za 4,0 pkt..............uzyskano

iennych, postaci pośrednie zależności) yv magazynie ień i

Pytanie 5.....

W dziedzinie stoch.

ych modeli planowania zasobów znana jest polityka (R,n). Proszę napisać równania ogólne będące podstawa, wyznaczania wartości zmiennych decyzyjnych R_p i n. W następnej kolejności proszę rozwiązać podane równania ogólne gdy zapotrzebowanie X na zasoby w odstępach czasu T określa rozkład normalny. Rozwiązań proszą poszukiwać dla poziomu p ryzyka, że rezerwa R_p okaże się niewystarczająca.

R-nie oqójne_t:

Vrvi W Ki

J3-

F

R-nie ooólne 2:

x

/f'P

<!«

Av\ '

VI¹

Rozwiązanie Qdv X ma rozkład normalny: i    I» -K-/4 |

Te cU

F \{

c    j_ę

Co

jj

d '

•^p-4' k

fl