bo2 (3)

Łącznie na 25,0 pkt uzyskano

pytanie 1.....................................................................................................za 2,5 pkt........

Proszę wygenerować 4 liczby losowe, o podanym niżej rozkładzie empirycznym p(z), W procesie generowania proszę przyjąć, że pierwsze cztery liczby z generatora liczb losowych o rozkładzie równomiernym na przedziale <0;1> są następujące: 0,49366353499; 0,73945614474; 0,85717559222; 0,76177534100.1

.uzyskano

’.0,05 0.35	dla dla	z = 10 z = 12	1 -sza liczba: 2-ea liczba:	aą-
0,40	dla	z = 14	3-cia liczba:	0,1
0,20	dla	z = 16	4-ta liczba:	m
e 2...

-1—f—i—f—

‘O ^/fż. 4Z{

-P

za 1,5 pkt..............uzyskano

Która z przedstawionych zależności jest matematycznym odwzorowaniem li-szei formuły Little’a (proszę zaznaczyć obwódką prawidłowe odpowiedzi) oraz objaśnić znaczenie użytych w tej zależności zmiennych.

♦ 7    = —_AV

^oczek.    ^Y oczek.

Objaśnienia zmiennych:

tóiutWp

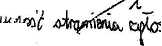
Loczek.    -^ocefc. ~ ^ ^oczek.

M

.uzyskano

M/M/n/Oj^ jeżeli czas między zgłoszeniami ma rozkład "^TDo wykonywania obsług zgłoszonych obiektów

Pytanie 3......................................................................................................za 2,0 pkt.

Proszę uzupełnić graf stanów jednofazowego systemu obsługowego wykładniczy o funkcji gęstości prawdopodobieństwa f(j) = źi-e przewidziano stanowisko obsługowe. Czas obsługi obiektów¹ na stanowisku ma rozkład wykładniczy o funkcji gęstości

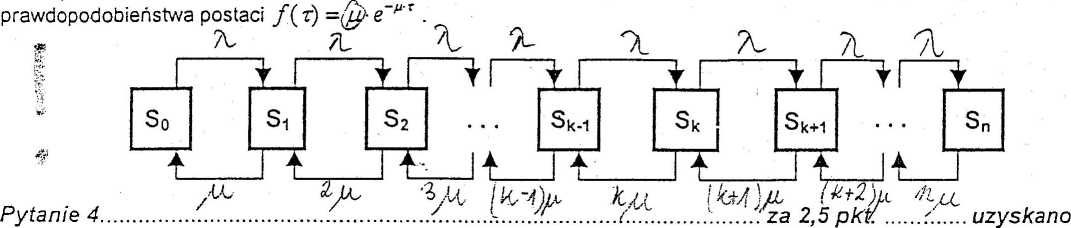
Proszę uzupełnić (schemat ideowy modelu, szkice pomocnicze, objaśnienie zmiennych, postaci pośrednie zależności) wyprowadzenie zależności na średni poziom niedoboru (braku) zasobów w magazynie w deterministycznym modelu ekonomicznej wielkości partii produkcyjnej w warunkach istnienia zaległych zamówień i planowych niedoborów zasobów .

Zależności pośrednie

Zależność początkowa: 1 ^T

=~\ n„{i)di

it

Szkice, objaśnienia:

5 ‘ni fbj cU

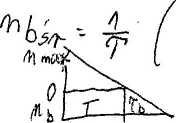
H

Zależność finalna:

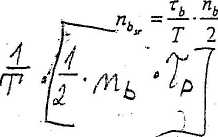
.uzyskano

W dziedzinie stochastycznych modeli planowania zasobów znana jest polityka (R,n). Proszę napisać równania ogólne będące podstawą wyznaczania wartości zmiennych decyzyjnych R_p i n. W następnej kolejności proszę rozwiązać podane równania ogólne gdy zapotrzebowanie X na zasoby w odstępach czasu T określa rozkład normalny. Rozwiązań proszę poszukiwać dla poziomu p ryzyka, że rezerwa R_p okaże się niewystarczająca.

R

■nie ogólne 1: P(_h-< j - F p

F?

R-nie ogólne 2:

■ FF

d_n_

U_w

kjjf.

i)^J

, dRZ

JCL

ol £p

ci»

-O

Rozwiązanie adv X ma rozkład normalny:

r-tb-Ą

f i n

t-i

-CL

M i

■i

't) * A

"1