CalkiTrygonometryczne2

CalkiTrygonometryczne2

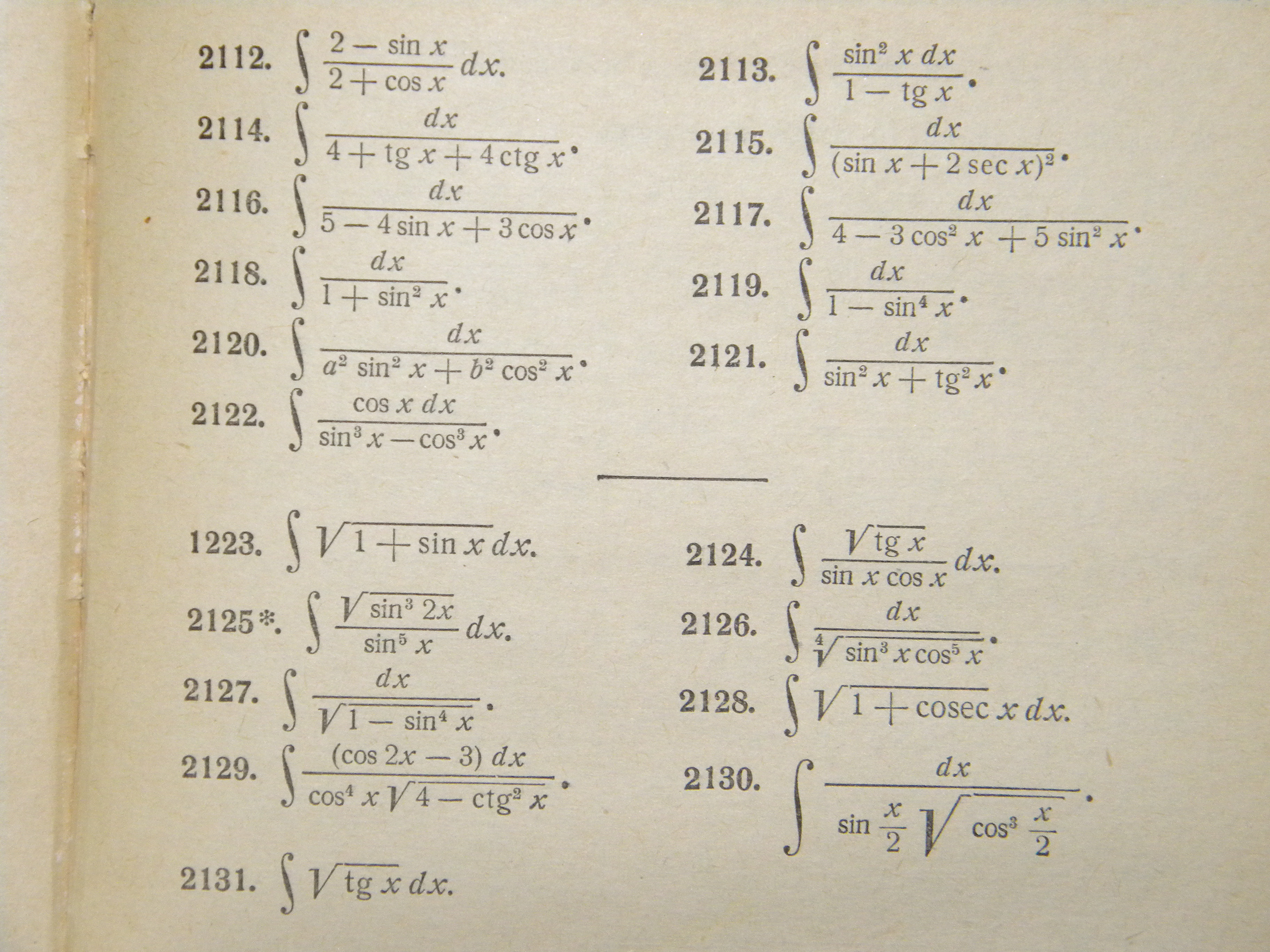
2112.

2114.

2116.

2118.

2120.

2122.

$

$

s

$

l

2 — sin x

o~i-dx.

2 + cos x

_dx_

4 + tg JKT + 4ctg JC*

_dx_

5 — 4 sin x + 3 cos# *

dx

1 + sin² x *

__djc_

a² sin² x + b² cos² x * cos x dx sin⁸ x—cos³ x*

1223.	^ ]/ 1 -j- sin x dx.
2125*	. C Ysin³ 2x j sin⁵ x	■dx.
2127.	ę dx
2127.	j Y1 — sin⁴	—- « a:
2129.	P (cos 2x —	3) rfjc
2129.	J cos⁴a:}^4~	- Ctg² X

2131. V V"tg xdx.

sin⁸ x dx 1 — tg a:

s

s

s

s

s

2113.

2115.

2117.

2119.

2121.

_dx_

(sin x + 2 sec *)⁸ *

__

4 —3 cos⁸ je -j- 5 sin⁸ x *

dx

1 — sin⁴ a: * dx

sin⁸je-|- tg⁸je*

2124.

2126.

2128.

s

s

s

V"tg

X

sin x cos x dx

dx.

sin³ x cos⁵ x^%

V1 -f- cosec x dx.

2130.

Wyszukiwarka

Podobne podstrony:
Image249 sin( &+ sm /f _ sin( &+ “ y—-——t “ ^ cos Ły
286 Z. KORUBA ET AL. Ivz — (A< T IprĘpv cos dpy T IprripV sin dpv) sin lfipv + “I- (+ ^prQpv ) C
IMGA67 &o< Ujl 2-y = Q ■ 6 M2 i ■ (V^> JńfcL Sin JU -y^i®) ]iBj- /) , 1
nego, z jednego satelity, na nośnej LI, Si(t) postaci Si(t) = APPi(t)Di(t) sin (27r/t + 0) + AcCi(t)
e**sin /3c, xe‘* sin/*,..., xk~leOK sin e‘* cosP<, xe‘M cos/3i.....xk~le‘* cos/3< są
AX Mf —d • c°s Ą*,,. =—95,542 m £HMF =d -sin    10,528/nAXMP"= (P-COS V= ~
75731 S6300966 e) Hm x3 arc ctg —; x—0~    x 1 — sin xg) lim ---? x—f   &nb
4. Naszkicować wykresy funkcji: 4.1. y = arc sin x, 4.2. y = arc tg x, 4.3. y = arc cos x. 4.4. y
skan0025 na 54.    u = C cos 4® -li- Ca sin 4® -ł- 3® sin 4® 55.    y
stany nieustalone str18 i{t) = C ^U(    sin(<2tf + y/ - ę?) w dt Z v   &
335 (12) 670 26. Analiza obwodów nieliniowych Przyjmujemy x — i, wobec tego dx v = — = fme “ (— x si
22 (3) Biblioteczka Opracowań Matematycznych 135/ ^ cin* dx sin‘xcosx sm x = t -= cosx = dx = dl -J7
d. 1: Obliczyć granicę stosując regułę de 1’Hospitala: sin(3x) lim x->0 ) lim x->0 X 1 - COS
rr4a 1= cos 0 +i sin 0 /fi = cosO + żsin 0 n = cos — + 2 sin2 = cos Et+ 2 sin Et3n . . 3EE = cos-+ 2

więcej podobnych podstron