CCF20090421002 (4)

3. A RyWuzyk-Pirek

5

Konstrukcja punktowych operacji symetrii

- ;    i

Tożsamość (operacja jednostkowa)

dowolna figura jest symetryczna względem tożsamości,

(każdy punkt przekształca się sam w siebie) J .

Symbol krystalograficzny l (wg Schoenfliesą C,) symbol graficzny: brak

reprezentacja graficzna

symbolika na tzw kole projekcji

O punkt przed płaszczyzną rysunku i

X punkt za płaszczyzną rysunku

Trzecia oś (tutaj oś Z) ustawiona prostopadle do rysunku

Symbol krystalograficzny ra (wg Schoenfliesą CJ symbol graficzny elememu symetrii _

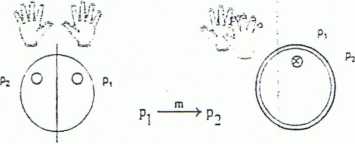
płaszczyzna odbicia    płaszczyzna oobicia

ustawiona prostopadle do rysunku    ustawiona równolegle do rysunku

(znajduje się w płaszczyźnie rysunku)

Odbicie w płaszczyźnie jest operacją symetrii 11-go rodzaju (odwrotną) - powstają obiekty chiralne (prawa i lewa dłoń)

3. AJtybuczyi-Ptrck    l i

Ograniczenia krotności osi obrotu w sieci przestrzennej wynikające z zachowania zasady translacji

Slech. będą dane 2 węzły sieci A i B lezące aa prostej sieciowej zgodnej z kjćruckienj X, odległe od siebie o odcinek długości periodu identyczności a.

Niech przez węzeł A sieci przechodzi oś ocrotu o kąt a. N'a skutek obrotu wenta B wocoł tej osi musi pojawić się węzeł C. Ze wzgiędu na periodyczr.csć sied oś taka przechodzić będzie rówruez przez węzeł B, a na skutek obrotu wotół mej musi pojawić się węzeł D

Oinnek GD jest równoległy do occuuca AB, zatem jego długość musi być wteiokrotnością długości AB

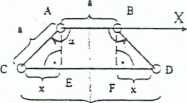
P»

3. ARyswrzźyk-Pirś

AB = a CD = pa = a -r 2x; p ć C xa - sin (a-90) = cos a =5 x = a cosa pa = a f 2(a cosa)

p = 1^T 2 cosa 'p> cosa = ( p - 1 y 2 17

Odbicie - operacja symetrii polegająca na odbiciu prostopadłym w płaszczyźnie (płaszczyzna s>mctni; płaszczyzna odbicia)

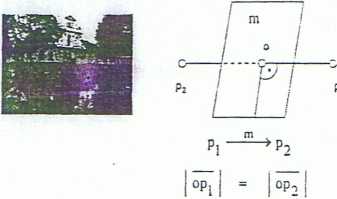
3. A RyaL.razyi-P.rck

Obrót (obrot właściwy; - operacja symetrii polegająca na obrocie o zadany kąt a wokół prostej (osi obrotu; Obrót następuje w płaszczyźnie prostopadłej do osi obrotu _n _L tt

n

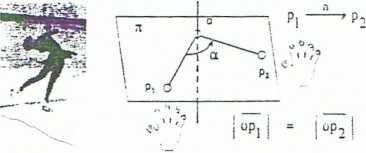
Syrnooi krystalograficzny n (wg Schoenfliesą C_a;

Obrót właściwy jest operacją symetrii i-go rodzaju (prostą) - nie zmienia się chirainość obiektu np. zawsze prawa diun

3 A Ryćtutt-Pru

Z rezwizin wyniki -i cosa = ( p - 1 ) / 2, gdzie psC Funkcji ccsinus przyjmuje winoscr w przecznic cosa c <-I; l>

-1 < cosa < 1

-i <(p-!)/2 < 1

-2 < p-1 <2

-1< p <3 i peC

p	cosa	a	a krotność os.
-1	-i	180 -	2
0	-1/-2	120 ^s	3
1	0	90 ^c	4
2	1/2	60 ^1	ć ■
3	.	0 =	1

Symbol krystalograficzny n :    1 (a = 360“) 2 (a - ISO')

3 (a =120“; 4(a = 9u“) 6 (a = 60“)

(w g Schoenfliesą C_a C, C₂ C₃ C, C₆)

V

i*-*